Tartalomjegyzék

Matematikai analízis III.

Az összes eddigi háttéranyagot ide próbálom összegyűjteni

Vektoranalízis

Matlab mintafeladatok és megoldásaik, melyek forráskódja (többnyire) a GitHub repository-ból is letölthetők:
1. Matlab segédlet, haladó szimbolikus műveletek Matlab-ban: deep_symbolic_tricks
2. Gradiens, divergencia, rotáció, Jacobi mátrix kiszámítása szimbolikusan
3. Különböző differenciálok, differenciálási szabályok, vonalintegrálok, felületintegrálok
4. segedszamitasok_2017_09_13_gyak1 (vonalintegrálok kiszámítása az 1. gyakorlatra)
5. segedszamitasok_2017_09_19_gyak2 (deriváltak szimbolikus kiszámítása)
6. segedszamitasok_2017_09_25_gyak3 (felületintegrálok)
7. anal3_cikloid_deltoid, Cycloid és a Deltoid.

Differenciálgeometria

Variációszámítás

Control systems demonstrations (CCS)

Inverted pendulum model (inverz inga modell)

1. Model description and derivation using calculus of variations: coming spoon.
2. Model linearization around stable and unstable equilibrium point, simulation and analysis.
3. Framework for the first Matlab practice
4. Model description and task sheet for the first Matlab practice: ccs_gyak08_matlabgyak1.pdf
5. Framework for the second Matlab practice
6. Model description and task sheet for the first Matlab practice: ccs_gyak08_matlabgyak2.pdf
7. Inverted pendulum control and integral reference tracking.
8. Inverted pendulum control and integral reference tracking (augmented, corrected).

Crane model (rakodó daru modellje)

1. Model description and derivation using calculus of variations (ccs_model_crane.pdf)
2. State space model derivation using symbolic computations
3. Simulink model and simulation (without control): sim_nonlinear_model_demo

Parciális differenciálegyenletek

Laplace egyenlet

1. Laplace egyenlet numerikus megoldása olyan tartományon és olyan peremfeltételekkel, amelyeket az órán is vettünk: pde_Laplace_2D_v2_gyaktipusu. $$ \begin{aligned} &u(0,y) = 0, && u(x,0) = 0,\\ &u(1,y) = 0, && u(x,1) = \sin(\pi x). \end{aligned} $$
2. Laplace egyenlet numerikus megoldása a képletben látható feltételek mellett. pde_Laplace_2D_v3_gyaktipusu $$ \begin{aligned} &u(0,y) = 0, && u'_y(x,0) = 0,\\ &u(1,y) = 0, && u(x,1) = f(x). \end{aligned} $$
3. Laplace egyenlet numerikus megoldása egy L alakú tartományon, bonyolultabb peremfeltételek mellett pde_Laplace_2D_v1.
4. Mathematica demonstráció: Laplace egyenlet szimbolikus megoldása, Fourier sorfejtés (ismétlés, kiegészítés)
5. Tavalyi demonstrációk: Laplace egyenlet numerikus megoldása érdekes peremfeltételek mellett (részletesen kommentezett Matlab kód).
   Ezt a PDE-t az assempde (vagyis asszem PDE) megoldó segítségével sikerült megoldani.

Hővezetés egyenlet

1. Hővezetés egyenlet gyenge megoldása végtelen hosszú rúd esetén (1D): pde_heat_transfer_1D_v2
2. Tavalyi demonstrációk: Hővezetés egyenlete 1D (+videó), Hővezetés egyenlete 2D (+videó)
3. Tavalyi demonstrációk: Hővezetés egyenlete véges rúdban különböző peremfeltételek mellett (matlab kód, annak részletes magyarázata és videók)
   Ebben a scriptben a pdepe solvert használtam, ami csak $u(x,t)$ időfüggő egyváltozós függvényekre működik ugyan, de a peremfeltételekket nagyon sokrétűen lehet variálni és a megoldás is kielégítően pontos.
   További megoldók: assempde, parabolic, hyperbolic, pdenonlin, ezekkel meg lehet oldani két-, háromdimenziós nem feltétlenül időfüggő feladatokat is, azonban itt még nem sikerült rájönnöm, hogyan kell klasszikus Neumann peremfeltételt megadni, ahol a norma menti derivált szerepel a megszorításban. A Matlab R2016a-ban ezeket a függvényeket egyesítették a solvepde függvényben.

Hullámegyenlet

1. Hullámegyenlet gyenge megoldása végtelen hosszú húr esetén (1D): dim1_hullam_vegtelen_rud_gyenge_megold_v1
2. Tavalyi demonstrációk: Egy rezgő membrán mozgásának szimulálása a hyperbolic solver segítségével.
3. Tsunami modellezés (forrás: Mathworks.com)

Nemlineáris egyenletek

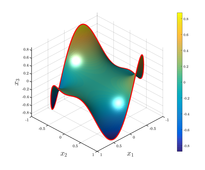
1. Minimális felületű szappanbuborék parciális differenciálegyenlete, mely ki van feszítve egy görbe drótkeretre (illusztráció).
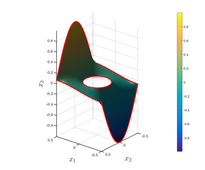
2. Minimális felületű szappanbuborék parciális differenciálegyenlete, mely ki van feszítve ket koncentrikus görbe drótkeretre (illusztráció).

Matematikai analízis III. (2017)

Események (ZH-k)

• október 19. - HF ZH
• október 27. - NagyZH
• november 30. - HF ZH
• december 14. - NagyZH

Gyakorlatok anyaga

anal3_01_17.pdf		1993 days		107.84 KB
anal3_02_17.pdf		1993 days		119.3 KB
anal3_03_17.pdf		1993 days		117.65 KB
anal3_04_17.pdf		1993 days		320.79 KB
anal3_05_17.pdf		1993 days		337.49 KB
anal3_06_17.pdf		1993 days		111.24 KB
anal3_07_17.pdf		1993 days		167 KB
anal3_08_17.pdf		1993 days		117.73 KB
anal3_09_17-izoperimetrikus_mo.pdf		1993 days		102.15 KB
anal3_09_17.pdf		1993 days		249.88 KB
anal3_10_17.pdf		1993 days		203.18 KB
anal3_11_17.pdf		1993 days		103.08 KB
anal3_12_17.pdf		1993 days		172.67 KB
anal3_kk_17.pdf		1993 days		2.04 MB

Matlabos konzi anyaga (2017. november 7.) itt található: anal3_2017_11_08_konzi.
Ehhez hasonló feladatok.

Beadott Matlabos szorgalmi házik

• Blazsek Martin János
  • elfajzott_torusz_alternativ
  • elfajzott_torusz_korrigalt
  • torusz
  • Multipólus erőtere és ennek integrálgörbéi

Matematikai analízis III. (2016)

Gyakorlatok anyaga

6ea_gorbe.pdf		1993 days		30.68 KB
anal3_01_16.pdf		1993 days		97.01 KB
anal3_01_16_kisbetu.pdf		1993 days		126.48 KB
anal3_01_16_v2.pdf		1993 days		131.51 KB
anal3_02_16.pdf		1993 days		180.74 KB
anal3_02_16_v2.pdf		1993 days		178.34 KB
anal3_03_16.pdf		1993 days		229.81 KB
anal3_04_16.pdf		1993 days		117.61 KB
anal3_05_15.pdf		1993 days		151.64 KB
anal3_05_16.pdf		1993 days		147.48 KB
anal3_05_16_v2.pdf		1993 days		143.67 KB
anal3_06_16.pdf		1993 days		180.52 KB
anal3_06_16_HF_ZH1.pdf		1993 days		77.39 KB
anal3_07_15.pdf		1993 days		115.33 KB
anal3_08_16.pdf		1993 days		160.04 KB
anal3_09_16.pdf		1993 days		119.93 KB
anal3_6het_HF_ZH1.pdf		1993 days		77.39 KB
anal3_10_16.pdf		1993 days		182.46 KB
anal3_11_16.pdf		1993 days		123.8 KB
anal3_11_16_HF_ZH2.pdf		1993 days		72.85 KB
anal3_12_16.pdf		1993 days		161.55 KB
anal3_13_16.pdf		1993 days		155.3 KB
anal3_nagyZH1.pdf		1993 days		114.56 KB
cycloid.pdf		1993 days		37.79 KB
deltoid.pdf		1993 days		34.68 KB
double_sided.pdf		1993 days		123.14 KB

Segédanyag, Matlab demonstrációk

Előző évek gyakorlatainak anyaga elérhető a Dropboxon.

hét. Vektoranalízis I.

• Elektromos terek (Coulumb törvénye alapján)
  • $Q_i$ ponttöltések $q$ negatív töltésre ható erőtere (vektormező)
  • Két elektromosan feltöltött fegyverzet $q$ pozitív töltésre ható erőtere (vektormező)
• Nehány feladat Matlabban megoldva
• Szimbolikus számítások Matlabban
• Vektormező integrálgörbéi (flow or integral curve of a vector field) illetve szintvonalai

hét. Vektoranalízis II.

• Néhány feladat Matlabban kiszámolva
• Skalárpontenciálos vektormezők a fizikában

hét. Vektoranalízis III.

• Néhány feladat Matlabban kiszámolva

hét. Variációszámítás I.

• Brachistochrone probléma megoldása (kézzel írott jegyzet)
• Brachistochrone - Matlab (E-L egyenletek, együtthatók kiszámítása)

hét. Variációszámítás II.

• Mathematica: Variációszámítás egy példa (Dido problémája)

hét. Variációszámítás III.

• Néhány feladat Matlabban kiszámolva

hét. NagyZH után, Matlab szimulációk.

• Brachistochrone probléma megoldása (kézzel írott jegyzet)
• Brachistochrone - Matlab (E-L egyenletek, együtthatók kiszámítása)
• Minimális felületű szappanbuborék parciális differenciálegyenlete, mely ki van feszítve egy görbe drótkeretre. (illusztráció)
• Minimális felületű szappanbuborék parciális differenciálegyenlete, mely ki van feszítve két koncentrikus görbe drótkeretre (budi). (illusztráció)

November 14. pótlás

• Az órán mutatott Matlab kód

hét. DiffGeó I.

Sokaságok, paraméteres, implicit megadás, normál tér, eríntőtér adott pontokban

Matlab demonstrációk

• Thomas A. Garrity, 6.1.1 Tétel bizonyításának demonstrációja Matlab-ban
  Mely szerint $k$ darab $n$ dimenziós $v_1,..,v_k$ vektor által kifeszített hipertér térfogata: $V = \sqrt{\det{A^T A}}$, ahol $A = [v1,..,v2] \in \mathbb{R}^{n \times k}$

hét. DiffGeó II. dformák, Stokes

hét. DiffGeó III., PDE I.

Mathematica demonstrációk

• Transzport egyenlet és elsőrendű PDE (az animáció html formában sajnos nem működik)

hét. PDE II.

Mathematica demonstrációk

• Laplace egyenlet, Fourier sorfejtés (ismétlés, kiegészítés)

hét. PDE III.

Matlab demonstrációk

• Hővezetés egyenlete 1D (+videó)
• Hővezetés egyenlete 2D (+videó)
• Ilyen extrém tartományokon is lehet PDE-t megoldani
• Nemlineáris PDE: lásd 7. hét: minimális felszínű felület (variációszámításból adódó PDE).

hét. PDE IV.

Matlab demonstrációk

• Hővezetés egyenlete véges rúdban különböző peremfeltételek mellett (matlab kód, annak részletes magyarázata és videók)
  Ebben a scriptben a pdepe solvert használtam, ami csak $u(x,t)$ időfüggő egyváltozós függvényekre működik ugyan, de a peremfeltételekket nagyon sokrétűen lehet variálni és a megoldás is kielégítően pontos.
  További megoldók: assempde, parabolic, hyperbolic, pdenonlin, ezekkel meg lehet oldani két-, háromdimenziós nem feltétlenül időfüggő feladatokat is, azonban itt még nem sikerült rájönnöm, hogyan kell klasszikus Neumann peremfeltételt megadni, ahol a norma menti derivált szerepel a megszorításban. A Matlab R2016a-ban ezeket a függvényeket egyesítették a solvepde függvényben.
• Laplace egyenlet numerikus megoldása érdekes peremfeltételek mellett (részletesen kommentezett Matlab kód).
  Ezt a PDE-t az assempde (vagyis asszem PDE) megoldó segítségével sikerült megoldani.
• Egy rezgő membrán mozgásának szimulálása a hyperbolic solver segítségével.

Kézzel írt jegyzetek PDE témakörben

Anal3_2nagyZH_2016_2bonusz_feladat_kidolgozasa.pdf		1993 days		540.17 KB
Elektromagneses_hullam_egyenletenek_levezetese_Maxwell_egyenletekbol.pdf		1993 days		284.69 KB
Hovezetes_egyenlete_kidolgozott_feladatok_energiamegmaradas.pdf		1993 days		3.04 MB
Vibrating_membrane_in_a_circular_domain.pdf		1993 days		58.74 KB

További segédanyagok, könyvek

Segédanyagok, könyvek

Brachistochrone_variacioszamitas_levezetes.pdf		1993 days		1.95 MB
PDE_ELTE_Besenyei.pdf		1993 days		3.64 MB
Stewart_Calculus_18ed_2015.pdf		1993 days		77.03 MB
Thomas_Calculus_11ed_2005.pdf		1993 days		33.08 MB
Thomas_Calculus_13ed_2014.pdf		1993 days		22.06 MB
megj_Gradiens_szintvonal_meroleges.pdf		1993 days		134.66 KB
megj_Gradiens_szintvonal_meroleges_2.pdf		1993 days		98.3 KB

Egyéb internetes források

www.stewartcalculus.com

MIT Open Course

• Multivariable calculus

Mathematica (software)

• Kalkulus
• Vektoranalízis
• PDE szimbolikus megoldása
• Variációszámítás: Függvények, Package

Wikipedia

• Electric potential - az elektromos tér $E = k_e\frac{Q}{\|r-r_Q\|^3}(r-r_Q)$ konzervatív, azaz potenciális, ezért létezik skalár-potenciálja: $U = - \int_\Gamma E \mathrm{d}r$, amire igaz, hogy: $\nabla U = -E$
• Magnetic potential
• Electric flux
• Gaussian surface
• Divergencia definíció
• Divergencia tétel
• Potential flow
• Lagrangian mechanics (variációszámítással kapcsolatos)
• Euler egyenletek (folyadék dinamika)