Tartalomjegyzék
\[ \newenvironment{dcases}{\left\{\begin{array}{ll}}{\end{array}\right.} \]Matematikai analízis III. (2011-18)
| Eloadas jegyzetek | ||||
| 0_Eloadas_jegyzetek_2011.pdf | 1972 days | 4.64 MB | ||
| 0_Eloadas_jegyzetek_2015-17.pdf | 1972 days | 1.65 MB | ||
| Kezzel irt jegyzetek (gakorlatvezetes) | ||||
| 1_Vekanal.pdf | 1972 days | 3.07 MB | ||
| 2_Diffgeom.pdf | 1972 days | 3.48 MB | ||
| 3_Varszam.pdf | 1972 days | 4.55 MB | ||
| 4_PDE.pdf | 1972 days | 2.93 MB | ||
| Egyebek | ||||
| 9_Piszkozatok.pdf | 1972 days | 215.92 KB | ||
| Ez igy mint egyetlen pdf-ben | ||||
| Anal3_kezzel_irt_jegyzetek_mind.pdf | 1972 days | 20.54 MB |
Matematikai analízis III. (2018)
Események (ZH-k)
- október 25. - 1. NagyZH (lejárt lemez)
- december 14. - 2. NagyZH (lejárt lemez)
- december 19. - javítóZH (lejárt lemez)
Beadandó házi feladatok rendje
Kötelező és csillagos házik. A lapon szereplő HF1, HF2 (ha lesz), Dn* és amiket esetleg említek az órán azok a következő hét gyakorlatán beadandóak. Utólag nem fogom elfogadni. A beadott HF megoldásokba utólag belekérdezhetek, ha valami nem egyértelmű.
Fizikai példák. A félév során 3-4 fizikai példa is fel lesz adva, ami egy kis rávezető a következő féléves "Infofiz" tantárgyra. Nehézségére és fontosságára való tekintettel az Fn*-os feladatokat később (a kiadás napjától számítva 3-4 hét múlva) is elfogadom, de idővel veszít értékéből ezt mindig pontosítani fogom a feladatkiírásban. A fizikai példákat az anal3_szorgalmi_1,2,3,4 pdf-ekben szereplő feladatok közül fogom szemezgetni. Ezen példáknál előfordulhat, hogy Matlab kódot is kell írni, ezt zippelve kérem feltölteni. Nem kizárt, hogy a szorgalmi pontszámok megjelenésére várni kell majd akár 2-3 hetet is.
FONTOS! Utolsó héten az áhított jegyre történő kerekítés reményében és kapkodva egy tucat pár sorban megoldott szorgalmi és/vagy csillagos feladat összevakarása nem fogja meghozni a remélt eredményt.
Házi feladatok beadásának módja. Amit csak lehet papíron adjátok le Vághy Mihálynak vagy nekem a hétfői órák szünetében. Ha valaki nagyon nem tudja leadni a házit papíron (mert pl. Luxorba utazott 3 hétre a fura bogarak tanulmányozása végett), akkor feltöltheti digitálisan is. Névkonvenciót szigorúan betartani: [hanyadik heti (lasd feladatsor cime) vagy melyik szorgalmi hazi]_[nev]_[megoldott feladat ha relevans].zip (szóközt, ékezetet NE tartalmazzon a fájl).
pl. 01_Almasi_Mate_F1.zip (elso heti feladatsorbol az F1* feladat megoldasa)
04_Godole_Istvan.zip (negyedik heti sima hazi + esetleges csillagos feladatok)A házi feladatok EZEN A LINKEN keresztül lehet feltölteni (ha nem működik azonnal írj e-mailt, kérlek).
Gyakorlatok anyaga, szorgalmi feladatok
| Gyakorlatok anyaga | ||||
| anal3_01_18.pdf | 2650 days | 529.74 KB | ||
| anal3_02_18_HF.pdf | 2650 days | 54.63 KB | ||
| anal3_03_18.pdf | 2650 days | 205.3 KB | ||
| anal3_04_18.pdf | 2650 days | 367.34 KB | ||
| anal3_05_18.pdf | 2650 days | 537.27 KB | ||
| anal3_06_18.pdf | 2650 days | 163.65 KB | ||
| anal3_07_18.pdf | 2650 days | 160.7 KB | ||
| anal3_08_18.pdf | 2650 days | 144.72 KB | ||
| anal3_09_18.pdf | 2650 days | 239.67 KB | ||
| anal3_10_18.pdf | 2650 days | 189.86 KB | ||
| anal3_11_18-print.pdf | 2648 days | 157.69 KB | ||
| anal3_11_18.pdf | 2598 days | 152.55 KB | ||
| anal3_12_18.pdf | 2641 days | 168.71 KB | ||
| anal3_gyakorlo_zh2_feladat_gyujt_17.pdf | 2645 days | 142.48 KB | ||
| Szorgalmi feladatok | ||||
| anal3_szorgalmi_1_vekanal.pdf | 2650 days | 644.29 KB | ||
| anal3_szorgalmi_2_diffgeom.pdf | 2650 days | 700.5 KB | ||
| anal3_szorgalmi_3_varszam.pdf | 2650 days | 318.81 KB | ||
| anal3_szorgalmi_4_pde.pdf | 2650 days | 19.9 KB |
Hasznos könyvek
Elsődleges irodalom: Thomas Garrity, All the mathematics you missed ...
| Joel_Broida_Calculus_of_Variations_and_Differential_Geometry_2009.pdf | 2650 days | 445.3 KB | ||
| Pavel_Grinfeld_Tensor_analysis.pdf | 2650 days | 1.88 MB | ||
| Robert_Weinstock_Calculus_Of_Variations_With_Apps_searchable.pdf | 2650 days | 13.83 MB | ||
| Simon_Malham_Lagrangian_Hamiltonian_mechanics.pdf | 2650 days | 685.86 KB | ||
| Thomas_Garrity_All_the_mathematics_you_missed_2002.pdf | 2650 days | 9.5 MB |
Kiegészítő anyag
Vektoranalízis
Matlab mintafeladatok és megoldásaik, melyek forráskódja (többnyire) a GitHub repository-ból is letölthetők:
1. Matlab segédlet, haladó szimbolikus műveletek Matlab-ban: deep_symbolic_tricks
2. Gradiens, divergencia, rotáció, Jacobi mátrix kiszámítása szimbolikusan
3. Különböző differenciálok, differenciálási szabályok, vonalintegrálok, felületintegrálok
Variációszámítás
Control systems demonstrations (CCS)
Inverted pendulum model (inverz inga modell)
- Model description and derivation using calculus of variations: coming spoon.
- Model linearization around stable and unstable equilibrium point, simulation and analysis.
- Framework for the first Matlab practice
- Model description and task sheet for the first Matlab practice: ccs_gyak08_matlabgyak1.pdf
- Framework for the second Matlab practice
- Model description and task sheet for the first Matlab practice: ccs_gyak08_matlabgyak2.pdf
- Inverted pendulum control and integral reference tracking.
- Inverted pendulum control and integral reference tracking (augmented, corrected).
Crane model (rakodó daru modellje)
- Model description and derivation using calculus of variations (ccs_model_crane.pdf)
- State space model derivation using symbolic computations
- Simulink model and simulation (without control): sim_nonlinear_model_demo
Parciális differenciálegyenletek
Laplace egyenlet
- Laplace egyenlet numerikus megoldása olyan tartományon és olyan peremfeltételekkel, amelyeket az órán is vettünk: pde_Laplace_2D_v2_gyaktipusu. $$ \begin{aligned} &u(0,y) = 0, && u(x,0) = 0,\\ &u(1,y) = 0, && u(x,1) = \sin(\pi x). \end{aligned} $$
- Laplace egyenlet numerikus megoldása a képletben látható feltételek mellett. pde_Laplace_2D_v3_gyaktipusu $$ \begin{aligned} &u(0,y) = 0, && u'_y(x,0) = 0,\\ &u(1,y) = 0, && u(x,1) = f(x). \end{aligned} $$
- Laplace egyenlet numerikus megoldása egy L alakú tartományon, bonyolultabb peremfeltételek mellett pde_Laplace_2D_v1.
- Mathematica demonstráció: Laplace egyenlet szimbolikus megoldása, Fourier sorfejtés (ismétlés, kiegészítés)
- Tavalyi demonstrációk: Laplace egyenlet numerikus megoldása érdekes peremfeltételek mellett (részletesen kommentezett Matlab kód).
Ezt a PDE-t az assempde (vagyisasszemPDE) megoldó segítségével sikerült megoldani.
Hővezetés egyenlet
- Hővezetés egyenlet gyenge megoldása végtelen hosszú rúd esetén (1D): pde_heat_transfer_1D_v2
- Tavalyi demonstrációk: Hővezetés egyenlete 1D (+videó), Hővezetés egyenlete 2D (+videó)
- Tavalyi demonstrációk: Hővezetés egyenlete véges rúdban különböző peremfeltételek mellett (matlab kód, annak részletes magyarázata és videók)
Ebben a scriptben a pdepe solvert használtam, ami csak $u(x,t)$ időfüggő egyváltozós függvényekre működik ugyan, de a peremfeltételekket nagyon sokrétűen lehet variálni és a megoldás is kielégítően pontos.
További megoldók: assempde, parabolic, hyperbolic, pdenonlin, ezekkel meg lehet oldani két-, háromdimenziós nem feltétlenül időfüggő feladatokat is, azonban itt még nem sikerült rájönnöm, hogyan kell klasszikus Neumann peremfeltételt megadni, ahol a norma menti derivált szerepel a megszorításban. A Matlab R2016a-ban ezeket a függvényeket egyesítették a solvepde függvényben.
Hullámegyenlet
- Hullámegyenlet gyenge megoldása végtelen hosszú húr esetén (1D): dim1_hullam_vegtelen_rud_gyenge_megold_v1
- Tavalyi demonstrációk: Egy rezgő membrán mozgásának szimulálása a hyperbolic solver segítségével.
- Tsunami modellezés (forrás: Mathworks.com)
Nemlineáris egyenletek
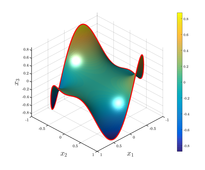
- Minimális felületű szappanbuborék parciális differenciálegyenlete, mely ki van feszítve egy görbe drótkeretre (illusztráció).
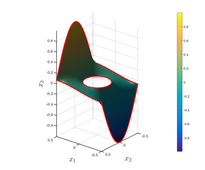
- Minimális felületű szappanbuborék parciális differenciálegyenlete, mely ki van feszítve ket koncentrikus görbe drótkeretre (illusztráció).
Előző évek anyagai, további kiegészítő anyagok