Tartalomjegyzék
\[ \newenvironment{dcases}{\left\{\begin{array}{ll}}{\end{array}\right.} \]A Laplace egyenlet megoldása egy L alakú tartományon
Teljes Matlab script kiegészítő függvényekkel.
file: pde_Laplace_2D_v1.m author: Polcz Péter <ppolcz@gmail.com>
Created on 2016.12.07. Wednesday, 15:58:30 Reviewed on 2017. November 30. [published]
Egyszerű peremfeltételek mellett
Az $\Omega$ tartomány létrhozása. A polygon tömb a tartomány sarkait tartalmazza: első oszlop $x$, második oszlop $y$ koordináták. A harmadik oszlop pedig az abból a sarokpontból a következő sarokpontban induló él konstants peremfeltételét tartalmazza, vagyis a (-1,0) pontból a (0,0) pontba futó élen a függvény értéke 0.2 kell legyen, a (0,0) pontból a (0,1) pontba futó élen a függvény -0.2 kell legyen, stb.
polygon = [
0 1 0
1 1 0
1 -1 0
-1 -1 0
-1 0 0.2
0 0 -0.2 ];
pdeGeom = geomDataFromPolygon(polygon(:,1:2));
PDE modell. Létrehozunk egy PDE modellt, ahol egyetlen függő változó van, az $u(x,y)$
numberOfPDE = 1;
pdem = createpde(numberOfPDE);
geometryFromEdges(pdem,pdeGeom);
Megjelenítés
figure('Position', [668 596 1012 377]); subplot(121)
pdegplot(pdem, 'edgeLabels', 'on'); axis equal
title('$\Omega$ tartomany, amelyen megoldom az egyenletet', 'Interpreter', 'latex');
plabel 'x' '$x$ tengely', plabel 'y' '$y$ tengely'
Az $i$-edig élen az $u(x,y)$ értéke polygon(i,3) kell legyen.
for i = 1:size(polygon,1);
applyBoundaryCondition(pdem,'Edge', i, 'u', polygon(i,3));
end

Az $\Omega$ tartomány felosztása, háromszögelés. A háromszögelés finomságát, sűrűségét a generateMesh Hmax tulajdonságával tudjuk szabályozni. A Hmax gyakorlatilag a háromszögek átmérőjének nagyságát szabályozza (megközelítőleg ekkorák lesznek a háromszögek.)
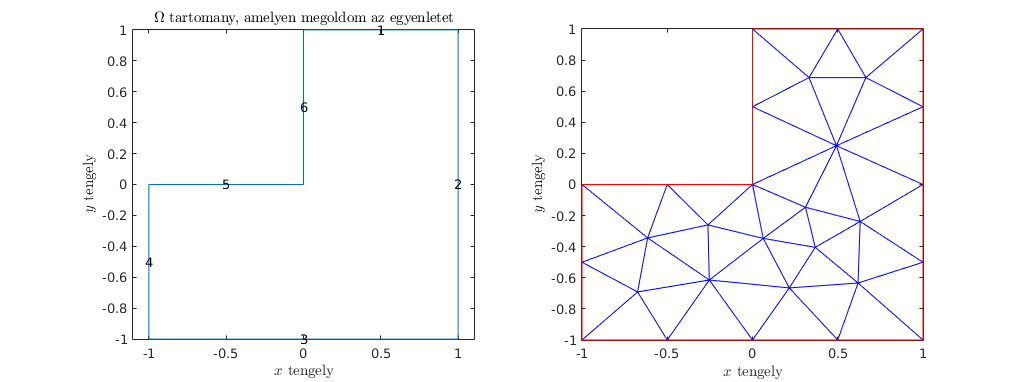
Durva háromszögelés
subplot(122); axis equal
title('$\Omega$ tartomany haromszogelve', 'Interpreter', 'latex');
msh = generateMesh(pdem,'Hmax',0.5);
pdemesh(pdem);
plabel 'x' '$x$ tengely', plabel 'y' '$y$ tengely'
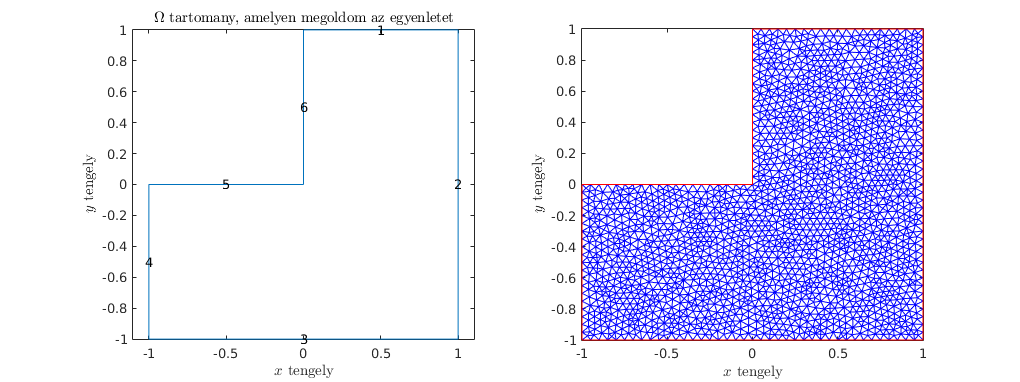
Finom háromszögelés
msh = generateMesh(pdem,'Hmax',0.05);
pdemesh(pdem);
plabel 'x' '$x$ tengely', plabel 'y' '$y$ tengely'
Megoldjuk az egyenletet
[u] = assempde(pdem,1,0,0);
Vizualizáció
[p,~,t] = meshToPet(msh);
figure('Position', [668 220 674 753]), hold on
trisurf(t(1:3,:)',p(1,:)',p(2,:)',u),
shading interp; light, axis square, view([ 233 , 34 ])
plabel 'x' '$x$ tengely', plabel 'y' '$y$ tengely'
edge = polygon(repmat(1:size(polygon,1),[2,1]), :);
edge = [edge(:,1:2) , circshift(edge(:,3),1)];
edge = [edge ; edge(1,:)];
plot3(edge(:,1), edge(:,2), edge(:,3),'r', 'LineWidth', 3)

Érdekesebb peremfeltételek mellett
Az $\Omega$ tartomány létrhozása. Marad a régi, csak a konstant peremfeltételek változtak (igazából lényegtelen milyen értékek szerepelnek ott, felül fogom írni őket).
polygon = [
0 1 0
1 1 NaN
1 -1 NaN
-1 -1 0
-1 0 0.2
0 0 -0.2 ];
pdeGeom = geomDataFromPolygon(polygon(:,1:2));
PDE modell. Létrehozunk egy PDE modellt, ahol egyetlen függő változó van, az $u(x,y,t)$. Itt sincs semmi változás.
numberOfPDE = 1;
pdem = createpde(numberOfPDE);
geometryFromEdges(pdem,pdeGeom);
Az $i$-edig élen az $u(x,y)$ értéke polygon(i,3) kell legyen.
for i = 1:size(polygon,1);
applyBoundaryCondition(pdem,'Edge', i, 'u', polygon(i,3));
end
További nem-konstants függvények, melyek Dirichlet feltételként fogok megfogalmazni adott peremeken.
bcfun2 = @(x,y) 0.05*sin(-2*pi*y);
bcfun2if = @(region,state) bcfun2(region.x, region.y);
bcfun3 = @(x,y) -0.2*(x.^2-1);
bcfun3if = @(region,state) bcfun3(region.x, region.y);
Nem-konstans Dirichlet feltételek
- $u(x,y) = f(x,y)$ típusú feltétel esetén az u-t kell megadni:
- $h(x,y)u(x,y) = r(x,y)$ típusú feltétel esetén a h és az r-t kell megadni:
- $n\cdot(c\times \nabla u(x,y)) + q(x,y) u(x,y) = g(x,y)$ típusú feltételek esetén csak a q és g függvényeket lehet megadni c-t nem, amit viszont alapértelmezetten nullának vesz. Így igazi Newmann peremfeltételt nem lehet megfogalmazni.
Lásd még: applyBoundaryCondition, Specify Nonconstant Boundary Conditions
applyBoundaryCondition(pdem,'Edge', 2, 'r', bcfun2if, 'h', 1);
applyBoundaryCondition(pdem,'Edge', 3, 'u', bcfun3if);
applyBoundaryCondition(pdem,'Edge', 4, 'q', 1, 'g', -0.1);
Háromszögelés és megoldjuk az egyenletet
msh = generateMesh(pdem,'Hmax',0.04);
[u] = assempde(pdem,1,0,0);
Vizualizáció
[p,~,t] = meshToPet(msh);
figure('Position', [668 220 674 753]), hold on
trisurf(t(1:3,:)',p(1,:)',p(2,:)',u),
shading interp; light, axis square, view([ 233 , 34 ])
plabel 'x' '$x$ tengely', plabel 'y' '$y$ tengely'
edge = polygon(repmat(1:size(polygon,1),[2,1]), :);
edge = [edge(:,1:2) , circshift(edge(:,3),1)];
edge = [edge ; edge(1,:)];
plot3(edge(:,1), edge(:,2), edge(:,3),'r', 'LineWidth', 3)
x = linspace(-1,1,100);
plot3(x*0+1,x,bcfun2(x,x),'r', 'LineWidth', 3);
plot3(x,x*0-1,bcfun3(x,x),'r', 'LineWidth', 3);
