Tartalomjegyzék
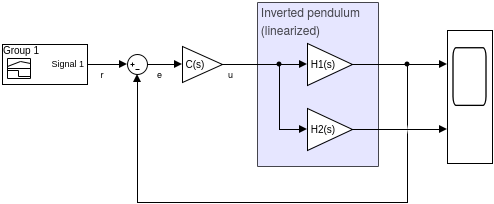
\[ \newenvironment{dcases}{\left\{\begin{array}{ll}}{\end{array}\right.} \]Inverted pendulum control and analysis
Teljes Matlab script kiegészítő függvényekkel.
file: ipend.m author: Peter Polcz <ppolcz@gmail.com>
Created on 2017.03.27. Monday, 17:42:37 Reviewed on 2017. October 30. [Published] Reviewed on 2017. November 08. [Corrected and published]
try c = evalin('caller','persist'); catch; c = []; end
persist = pcz_persist(mfilename('fullpath'), c); clear c;
persist.backup();
%clear persist
global PUBLISH
PUBLISH = 1;
Output:
│ - Persistence for `ipend1` reused (inherited) [run ID: 48, 036]Persistence for `2017.11.09. Thursday, 11:25:23` │ - Script `ipend1` backuped
A. Linearize around the stable equilibrium point
State space model
% model parameters
M = 0.5;
m = 0.2;
l = 1;
g = 9.8;
b = 0;
A = [
0 1 0 0
0 -(4*b)/(4*M + m) -(3*g*m)/(4*M + m) 0
0 0 0 1
0 -(3*b)/(l*(4*M + m)) -(3*g*(M + m))/(l*(4*M + m)) 0
];
B = [
0
4/(m+4*M)
0
3/(m+4*M)/l
];
C = [
1 0 0 0
0 0 1 0
];
D = [ 0 ; 0 ];
1. determine the transfer function of the system
sys = ss(A,B,C,D);
H = tf(sys);
H_r = H(1)
H_phi = H(2)
Output:
H_r =
1.818 s^2 + 13.36
-----------------
s^4 + 9.355 s^2
Continuous-time transfer function.
H_phi =
1.364
-----------
s^2 + 9.355
Continuous-time transfer function.
2. determine the impulse response of the system
T = 5;
[y,t] = impulse(H,T);
ipend_simulate_Pi(t,y)
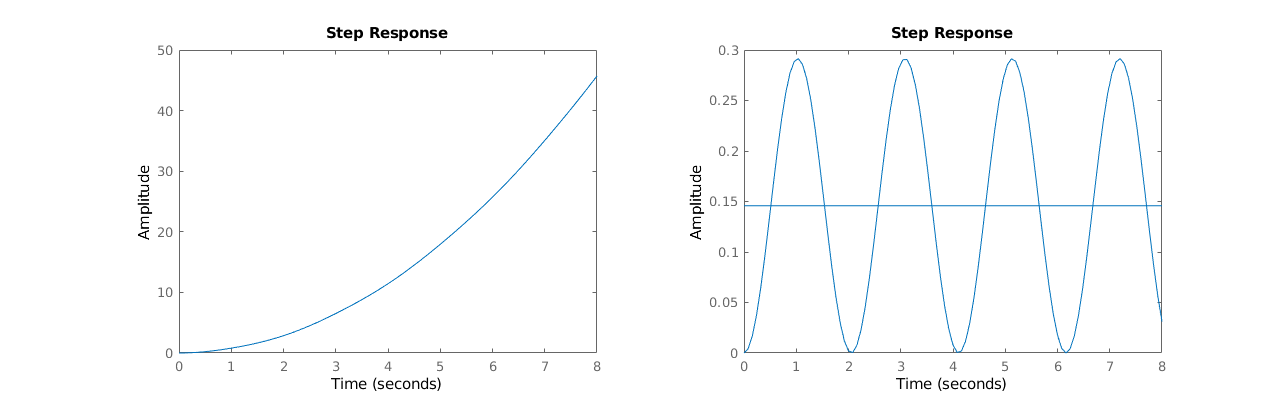
3. determine the step response and the DC gain of the system
T = 8;
figure('Position', [ 226 318 1276 392 ], 'Color', [1 1 1])
subplot(121)
step(H_r,T)
subplot(122)
step(H_phi,T), hold on
DC_gain = dcgain(H_phi);
plot([0 T],[1 1]*DC_gain)
Simulate
[y,t] = step(H,T);
ipend_simulate_Pi(t,y)
4. determine the poles of the system
Is the system stable, exponentially stable or unstable
eig(A)
Output:
ans = 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 3.0585i 0.0000 - 3.0585i
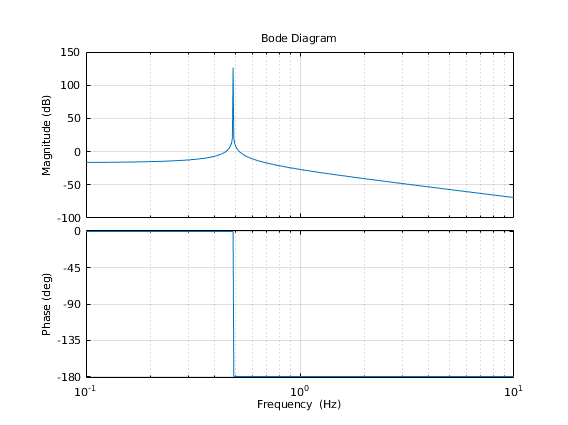
5. determine the Bode plot of the transfer function
Plot only for the transfer function from F to omega. The frequency unit set to be in Hz. Determine the own (or resonance) frequency (f_r) of the system.
figure
bopts = bodeoptions;
bopts.FreqUnits = 'Hz';
% bopts.FreqScale = 'linear';
% bopts.MagUnits = 'abs';
bodeplot(H_phi, bopts), grid on
[gpeak,fpeak] = getPeakGain(H_phi);
fr = fpeak / (2*pi)
Output:
fr =
0.4868
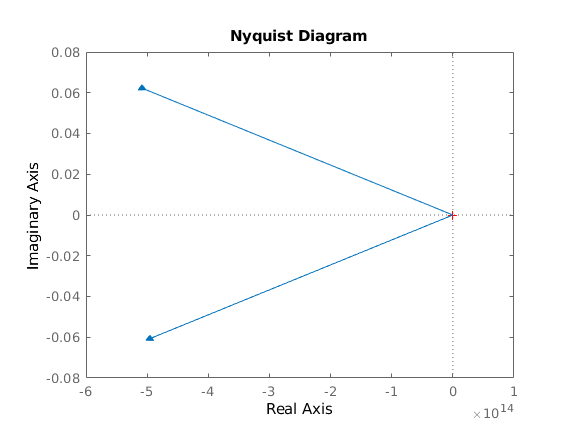
6. Nyquist plot
figure(6), nyquist(H_phi)
7. (a) Simulation using lsim - resonance frequency
T = 20;
Ts = 0.01;
t = 0:Ts:T;
f = fr;
Amp = 1;
u = Amp*sin(2*pi*f*t);
y = lsim(H,u,t);
ipend_simulate_Pi(t,y,u);
% After a while we shall notice, that the system's motion is quite
% unusual, why?
7. (b) Simulation using lsim - high frequency, large amplitude
T = 10;
Ts = 0.01;
t = 0:Ts:T;
f = 4;
Amp = 20;
u = Amp*sin(2*pi*f*t)-0.1;
y = lsim(H,u,t);
ipend_simulate_Pi(t,y,u);
7. (c) Simulation using lsim - low frequency
T = 20;
Ts = 0.01;
t = 0:Ts:T;
f = 0.1;
Amp = 1;
u = Amp*sin(2*pi*f*t + pi/2);
y = lsim(H,u,t);
ipend_simulate_Pi(t,y,u);
8. Simulation using ode45
x0 = [0 0 pi/6 0]';
u = 0;
T = 5;
[t,x] = ode45(@(t,x) A*x + B*u, [0 T], x0);
ipend_simulate_Pi(t,x)
9. Controllability
C4 = [ B A*B A*A*B A*A*A*B ]
C4_ = ctrb(A,B);
rank(C4)
Output:
C4 =
0 1.8182 0 -3.6446
1.8182 0 -3.6446 0
0 1.3636 0 -12.7562
1.3636 0 -12.7562 0
ans =
4
10. Observability
C = [
1 0 0 0
0 0 1 0
];
O4 = obsv(A,C)
O4_ = ctrb(A',C')'
rank(O4)
% Measure only phi
C = [ 0 0 1 0 ];
O4 = obsv(A,C);
S = [ orth(O4) null(O4) ];
T = inv(S);
A_ = T*A/T
B_ = T*B
C_ = C/T
Output:
O4 =
1.0000 0 0 0
0 0 1.0000 0
0 1.0000 0 0
0 0 0 1.0000
0 0 -2.6727 0
0 0 -9.3545 0
0 0 0 -2.6727
0 0 0 -9.3545
O4_ =
1.0000 0 0 0
0 0 1.0000 0
0 1.0000 0 0
0 0 0 1.0000
0 0 -2.6727 0
0 0 -9.3545 0
0 0 0 -2.6727
0 0 0 -9.3545
ans =
4
A_ =
0 -1.0000 0 0
9.3545 0 0 0
0 0 0 -1.0000
3.6519 0 0 0
B_ =
0
1.3714
0
1.9640
C_ =
-0.9943 0 0 0
B. Nonlinear model. No friction
Input affine model
$$\dot x = f(x) + g(x) u$$
syms t x v phi omega
% model parameters
M = 0.5;
m = 0.2;
l = 1;
g = 9.8;
b = 0;
q = 4*(M+m) - 3*m*cos(phi)^2;
f_sym = [
v
(4*m*l*sin(phi)*omega^2 - 1.5*m*g*sin(2*phi) -4*b*v) / q
omega
3*(-m*l*sin(2*phi)*omega^2 / 2 + (M+m)*g*sin(phi) + b*cos(phi)*v) / (l*q)
];
g_sym = [
0
4*l
0
-3*cos(phi)
] / (l*q);
f_ode = matlabFunction(f_sym, 'vars', {t , [ x ; v ; phi ; omega ]});
g_ode = matlabFunction(g_sym, 'vars', {t , [ x ; v ; phi ; omega ]});
11. Simulation with no input
[tt,xx] = ode45(f_ode, [0,10], [0 0 0.1 0]');
ipend_simulate_0(tt,xx)
[tt,xx] = ode45(f_ode, [0,10], [0 0 0.1 2]');
ipend_simulate_0(tt,xx)
11. Simulation with large amplitude high frequency sinusoidal signal
Ampl = 20;
f = 4;
u = @(t) Ampl*sin(2*pi*f*t);
[tt,xx] = ode45(@(t,x) f_ode(t,x) + g_ode(t,x)*u(t), [0,5], [0 0 pi 0]');
ipend_simulate_0(tt,xx,u)
11. Simulation with small amplitude own frequency sinusoidal signal
Ampl = 1;
f = fr;
u = @(t) Ampl*sin(2*pi*f*t);
[tt,xx] = ode45(@(t,x) f_ode(t,x) + g_ode(t,x)*u(t), [0,30], [0 0 pi 0]');
ipend_simulate_0(tt,xx,u)
11. Simulation with small amplitude low frequency sinusoidal signal
Ampl = 1;
f = 0.1;
u = @(t) Ampl*sin(2*pi*f*t + pi/2);
[tt,xx] = ode45(@(t,x) f_ode(t,x) + g_ode(t,x)*u(t), [0,30], [0 0 pi 0]');
ipend_simulate_0(tt,xx,u)
C. Nonlinear model. With friction
Input affine model
$$\dot x = f(x) + g(x) u$$
syms t x v phi omega
% model parameters
M = 0.5;
m = 0.2;
l = 1;
g = 9.8;
b = 10;
q = 4*(M+m) - 3*m*cos(phi)^2;
f_sym = [
v
(4*m*l*sin(phi)*omega^2 - 1.5*m*g*sin(2*phi) -4*b*v) / q
omega
3*(-m*l*sin(2*phi)*omega^2 / 2 + (M+m)*g*sin(phi) + b*cos(phi)*v) / (l*q)
];
g_sym = [
0
4*l
0
-3*cos(phi)
] / (l*q);
f_ode = matlabFunction(f_sym, 'vars', {t , [ x ; v ; phi ; omega ]});
11. Simulation
[t,x] = ode45(f_ode, [0,10], [0 0 pi/12 2]');
ipend_simulate_0(t,x)
D. Linear model with friction PID controller
State space model
model parameters
M = 0.5;
m = 0.2;
l = 1;
g = 9.8;
b = 0;
A = [
0 1 0 0
0 -(4*b)/(4*M + m) -(3*g*m)/(4*M + m) 0
0 0 0 1
0 -(3*b)/(l*(4*M + m)) -(3*g*(M + m))/(l*(4*M + m)) 0
];
B = [
0
4/(m+4*M)
0
3/(m+4*M)/l
];
C = [
1 0 0 0
0 0 1 0
];
D = [ 0 ; 0 ];
Transfer function of the system
sys = ss(A,B,C,D);
H = tf(sys);
H_r = H(1);
H_phi = H(2);
PID for the non-inverted pendulum, reference tracking
Only if $b \not= 0$!
open_system ipend_PID_demo
print -dpng fig/ipend_PID.png -sipend_PID_demo
C_r = pidtune(H_r,'pid');
% pidTuner(H_r,C_r)
At home: derive the resulting transfer function
Control_Loop = [
C_r*H_r / (1 + C_r*H_r)
C_r*H_phi / (1 + C_r*H_r)
];
T = 20;
t = linspace(0,T,T/0.1);
u = t*0 + 5;
y = lsim(Control_Loop,u,t);
ipend_simulate_Pi(t,y)