Tartalomjegyzék
\[ \newenvironment{dcases}{\left\{\begin{array}{ll}}{\end{array}\right.} \]Inverted pendulum control and reference tracking (servo)
Teljes Matlab script kiegészítő függvényekkel.
file: ipend2.m author: Peter Polcz <ppolcz@gmail.com>
Created on 2017.05.02. Tuesday, 22:39:05 Reviewed on 2017. November 22. [servo control]
try c = evalin('caller','persist'); catch; c = []; end
persist = pcz_persist(mfilename('fullpath'), c); clear c;
persist.backup();
%clear persist
global PUBLISH
PUBLISH = 1;
Output:
│ - Persistence for `ipend2` reused (inherited) [run ID: 48, 120]Persistence for `2017.11.22. Wednesday, 17:35:57` │ - Script `ipend2` backuped
Nonlinear model - parameters (A)
No friction
syms t x v phi omega
% model parameters
M = 0.5;
m = 0.2;
l = 1;
g = 9.8;
b = 0;
q = 4*(M+m) - 3*m*cos(phi)^2;
f_sym = [
v
(4*m*l*sin(phi)*omega^2 - 1.5*m*g*sin(2*phi) -4*b*v) / q
omega
3*(-m*l*sin(2*phi)*omega^2 / 2 + (M+m)*g*sin(phi) + b*cos(phi)*v) / (l*q)
];
g_sym = [
0
4*l
0
-3*cos(phi)
] / (l*q);
f_ode = matlabFunction(f_sym, 'vars', {t , [ x ; v ; phi ; omega ]});
g_ode = matlabFunction(g_sym, 'vars', {t , [ x ; v ; phi ; omega ]});
Linearized model around the unstable equilibrium point
% model parameters
M = 0.5;
m = 0.2;
l = 1;
g = 9.8;
b = 0;
A = [
0 1 0 0
0 -(4*b)/(4*M + m) -(3*g*m)/(4*M + m) 0
0 0 0 1
0 (3*b)/(l*(4*M + m)) (3*g*(M + m))/(l*(4*M + m)) 0
];
B = [
0
4/(m+4*M)
0
-3/(m+4*M)/l
];
C = [
1 0 0 0
0 0 1 0
];
D = [ 0 ; 0 ];
sys = ss(A,B,C,D);
K = place(A,B,-4:-1);
pcz_num2str(K)
K = lqr(A,B,eye(4),1);
pcz_num2str(K)
L = place(A',C',-4:0.1:-3.7)'
pcz_num2str(L)
Output:
[ -1.7959 , -3.7415 , -34.9212 , -12.322 ]
[ -1 , -2.2428 , -26.6075 , -9.3028 ]
L =
7.6382 0.0811
14.5773 -2.3605
0.0761 7.7618
0.2935 24.4073
[ 7.6382 , 0.0811 ; 14.5773 , -2.3605 ; 0.0761 , 7.7618 ; 0.2935 , 24.4073 ]
Transfer function of the closed loop system
Ac = [ A-B*K B*K ; zeros(4,4) A-L*C ];
Bc = [ B ; zeros(4,1) ];
Cc = [ 1 0 0 0 -1 0 0 0 ];
Dc = 0;
cls = ss(Ac,Bc,Cc,Dc);
Ge = minreal(tf(cls))
pzmap(Ge)
Gi = pidtune(Ge,'I')
G_all = minreal(Ge*Gi / (1 + Ge*Gi));
Output:
Ge =
1.818 s^2 + 3.23e-15 s - 13.36
---------------------------------------------
s^4 + 8.608 s^3 + 25.11 s^2 + 29.97 s + 13.36
Continuous-time transfer function.
Gi =
1
Ki * ---
s
with Ki = -0.241
Continuous-time I-only controller.

Linear-Quadratic-Integral control: lqi
C = [
1 0 0 0
];
D = [ 0 ];
sys = ss(A,B,C,D);
K_lqi = lqi(sys, 1*eye(5),1);
K = -K_lqi(:,1:4);
Ki = K_lqi(end);
% set_param('ipend2_sim_servo/K','Gain',pcz_num2str(K))
% set_param('ipend2_sim_servo/Ki','Gain',num2str(Ki))
set_param('ipend2_sim_servo/K_lqi','Gain',pcz_num2str(-K_lqi))
Simulate simulink results
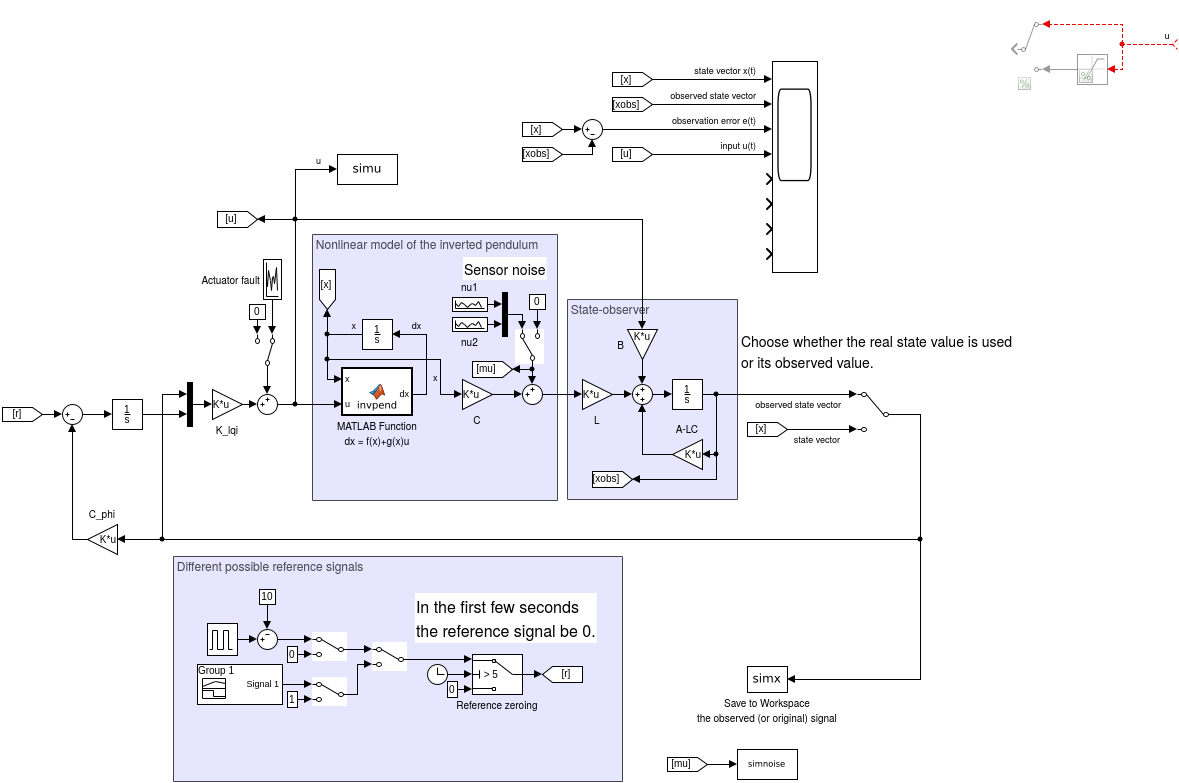
Simulink model (ipend2_sim_servo.slx)
open_system ipend2_sim_servo
print -dpng fig/ipend2_sim_servo.png -sipend2_sim_servo
Simulate and visualize external control force
t = simx.Time;
x = simx.Data;
u = simu.Data;
ipend_simulate_0(t,x,u)
return
Just simulate
t = simx.Time;
x = simx.Data;
ipend_simulate_0(t,x)
T = 100;
N = 100;
t = linspace(0,T,N);
r = zeros(size(t));
r(30:70) = 1;
simr = [ t' r' ];