Contents
file: pde_wave_equation_2D.m author: Polcz Péter <ppolcz@gmail.com>
Created on 2016.12.15. Thursday, 21:54:27
% fname: full path of the actual file pcz_cmd_fname('fname'); stack = dbstack; if ~ismember('publish', {stack.name}), persist = pcz_persist(fname); end %persist.backup();
Rezgő membrán szimulációja
A hullámegyenlet segítségével szimulálni tudjuk egy rezgő membrán mozgását különböző alakú tartományok és peremfeltételek esetén.
A hullám egyenlete:
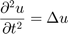
Ez egy hiperbolikus PDE, amelynek numerikus megoldását a PDE Toolbox hyperbolic függvényével számoljuk ki. A hyperbolic megoldó
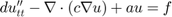
ahol a 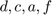 lehetnek függvényei az időnek
és a pozíciónak (x,z) is. A mi
esetünkben:
lehetnek függvényei az időnek
és a pozíciónak (x,z) is. A mi
esetünkben:
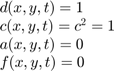
d = 1; c = 1; a = 0; f = 0;
PDE modell. Létrehozunk egy PDE modellt, ahol
egyetlen függő változó van, az
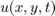
numberOfPDE = 1; pdem = createpde(numberOfPDE);
Az 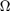 tartomány létrhozása.
tartomány létrhozása.
Két lehetséges tartományt is definiálunk (a megfelelőt kell kikommentezni).
![$\Omega_1 = [-1,1]^2$](pde_wave_equation_2D_eq02561636244914411334.png) négyzetes
tartomány
négyzetes
tartomány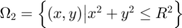 körtartomány
körtartomány
% [Omega1] pdeGeom = geomDataFromPolygon([-1 -1 ; -1 1 ; 1 1 ; 1 -1]); % [Omega2] pdeGeom = geomDataOfCircularHoles([0,0,1]); geometryFromEdges(pdem,pdeGeom); figure('Position', [668 596 1012 377]); subplot(121) pdegplot(pdem, 'edgeLabels', 'on'); axis([-1.1 1.1 -1.1 1.1]); title('$\Omega$ tartomany, amelyen megoldom az egyenletet', 'Interpreter', 'latex');
Az 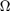 tartomány felosztása,
háromszögelés. A
háromszögelés finomságát,
sűrűségét a generateMesh
Hmax tulajdonságával tudjuk
szabályozni. A Hmax gyakorlatilag a
háromszögek átmérőjének
nagyságát szabályozza
(megközelítőleg ekkorák lesznek a
háromszögek.)
tartomány felosztása,
háromszögelés. A
háromszögelés finomságát,
sűrűségét a generateMesh
Hmax tulajdonságával tudjuk
szabályozni. A Hmax gyakorlatilag a
háromszögek átmérőjének
nagyságát szabályozza
(megközelítőleg ekkorák lesznek a
háromszögek.)
msh = generateMesh(pdem,'Hmax',0.1); subplot(122), pdemesh(pdem); axis equal title('$\Omega$ tartomany felosztasa', 'Interpreter', 'latex');
Peremfeltételek
A peremfeltételek esetén is megadok két különböző variációt:
- A két szélső perem ne legyen megkötve (itt a membrán szabadon mozoghat). A membrán másik két oldala legyen rögzített, vagyis itt a hullámfüggvény értéke mindig 0.
- A membrán minden oldal ki van feszítve,
azaz
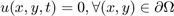
% [1] applyBoundaryCondition(pdem,'Edge',([1 3]), 'g', 0); applyBoundaryCondition(pdem,'Edge',([2 4]), 'u', 0); % [2] applyBoundaryCondition(pdem,'Edge',1:4, 'u', 0);
Kezdeti feltételek
Az eredeti scriptben a következő kezdeti feltételek voltak megadva:
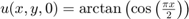 .
. .
.
A script eredeti szerzői így magyarázzák ezt a választást: "This choice avoids putting energy into the higher vibration modes and permits a reasonable time step size."
Én alapvetően azt szerettem volna
szimulálni, hogy membrán közepére
ütünk egy hatalmasat, ezt nem nehéz
szimulálni (elfajúló haranggörbe).
Azonban az 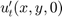 kezdeti feltétel esetén nem volt
jobb ötletem mint azt mondani, hogy ez legyen nulla. Egy
interneten talált leírásban is
végeznek hasonló kísérletet:
Vibrating
membrane in a circular domain
kezdeti feltétel esetén nem volt
jobb ötletem mint azt mondani, hogy ez legyen nulla. Egy
interneten talált leírásban is
végeznek hasonló kísérletet:
Vibrating
membrane in a circular domain
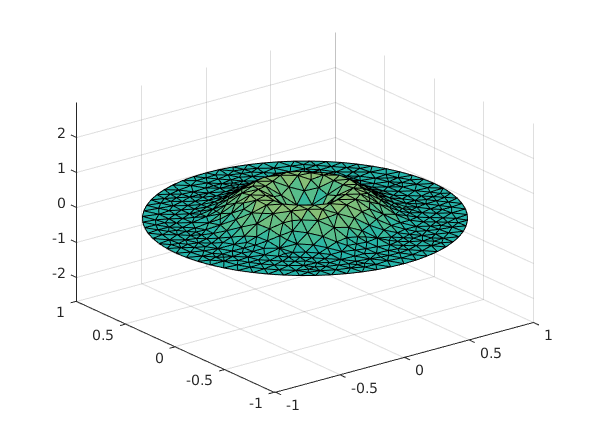
s = 4; [p,~,t] = meshToPet(msh); x = p(1,:)'; y = p(2,:)'; % Általam definiált kezdeti feltétel u0 = 3*exp(- s^2*(x.^2 + y.^2)); ut0 = x*0; % Eredeti kezdeti feltétel % u0 = atan(cos(pi/2*x)); % ut0 = 3*sin(pi*x).*exp(sin(pi/2*y)); figure('Position', [342 452 1316 433]), subplot(121) trisurf(t(1:3,:)', p(1,:), p(2,:), u0) title('$u(x,y,0)$ kezdeti feltetel','Interpreter','latex') subplot(122), trisurf(t(1:3,:)', p(1,:), p(2,:), ut0); title('$u''_t(x,y,0)$ kezdeti feltetel','Interpreter','latex')

Egyenlet megoldása
% Idő diszkretizálása
T = 5;
n = 201;
tlist = linspace(0,T,n);
uu = hyperbolic(u0,ut0,tlist,pdem,c,a,f,d);
1111 successful steps 116 failed attempts 2456 function evaluations 1 partial derivatives 301 LU decompositions 2455 solutions of linear systems
Animáció
figure umax = max(max(uu)); umin = min(min(uu)); for i = 1:n trisurf(t(1:3,:)', p(1,:), p(2,:), uu(:,i)); axis([-1 1 -1 1 umin umax]); caxis([umin umax]); if i == 10 persist.pub_vid_poster('membran_rezgomozgas') end M(i) = getframe; end persist.pub_vid_write(M) if ismember('publish', {stack.name}), return; end