Contents
Hővezetés egyenlete véges rúdban különböző peremfeltételek mellett
file: pde_heat_transfer_finite_triangle.m author: Polcz Péter <ppolcz@gmail.com>
Created on 2016.12.15. Thursday, 13:11:44
% fname: full path of the actual file pcz_cmd_fname('fname'); stack = dbstack; if ~ismember('publish', {stack.name}), persist = pcz_persist(fname); end %persist.backup();
Hővezetés egyenlete: 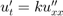 , ahol
, ahol 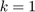 .
.
Kezdeti feltételek:
![$$u(x,0) = \left\{\begin{array}{lc} x & x \in \left[0,\frac{1}{2}\right) \\[10pt] 1-x & x \in \left[\frac{1}{2},1\right] \end{array}\right.$$](pde_heat_transfer_finite_triangle_eq18163358398576811382.png)
Peremfeltételek:
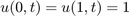
A pdepe solver
A pdepe solver ilyen típusú kétváltozós PDE-ket tud megoldani:
![$$ \left\{ \begin{array}{l} c(x,t,u,u'_x) u'_t = x^{-m} \Big(x^m f(x,t,u,u'_x)\Big)'_x + s(x,t,u,u'_x) \\[5pt] {\rm i.c.}~~ u(x,t_0) = u_0(x) \\[5pt] {\rm b.c.}~~ p_1(x_1,t,u(x_1,t)) + q(x_1,t) f(x_1,t,u(x_1,t),u'_x(x_1,t)) = 0, \quad \forall t > t_0 \\[5pt] {\rm b.c.}~~ p_2(x_2,t,u(x_2,t)) + q(x_2,t) f(x_2,t,u(x_2,t),u'_x(x_2,t)) = 0, \quad \forall t > t_0 \end{array} \right.$$](pde_heat_transfer_finite_triangle_eq06381263307276912244.png)
Az 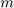 értéke csak 0,1,2, lehet.
értéke csak 0,1,2, lehet.
A pdepe első paramétere az 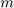 értéke (esetünkben 0), a
második paramétere a
értéke (esetünkben 0), a
második paramétere a  ,
, 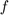 ,
,  függvényeket írja le, a harmadik
paramétere az
függvényeket írja le, a harmadik
paramétere az 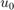 , a negyedik pedig a
, a negyedik pedig a 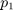 ,
, 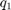 ,
, 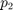 ,
, 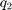 függvényeket írjak le. A
következő két paraméter az
függvényeket írjak le. A
következő két paraméter az  és a
és a 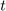 diszkrét pontjait
definiálják.
diszkrét pontjait
definiálják.
A hővezetés egyenlet együtthatói együtthatói:
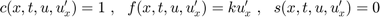
k = 1;
% The equation of the problem.
pde = @(x,t,u,DuDx) deal( 1 , k*DuDx , 0);
Az előző sor kissé mélyvíznek
tűnhet a kezdő Matlab felhasználóknak.
A pde egy olyan anoním függvény
kell hogy legyen, aminek négy argumentuma van: 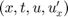 , és három
visszatérési értéke:
, és három
visszatérési értéke:  ,
, 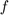 ,
,  . A deal függvény oldja meg azt,
hogy egy inline deklarált anoním
függvénynek több (esetünkben
három) visszatérési értéke
legyen. Ezzel ekvivalens módon létre is hozhattam
volna egy külön file-ban egy
függvényt:
. A deal függvény oldja meg azt,
hogy egy inline deklarált anoním
függvénynek több (esetünkben
három) visszatérési értéke
legyen. Ezzel ekvivalens módon létre is hozhattam
volna egy külön file-ban egy
függvényt:
function [c,f,s] = pde_fun(x,t,u,DuDx) c = 1; f = k*DuDx; s = 0; end
A scriptben pedig: pde = @pde_fun. Ezt szerettem volna elkerülni.
% Initial condition:
ic = @(x) triangularPulse(0,1,x);
A peremfeltételeket a következő alakban kell megadni:
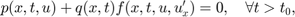
ahol 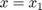 (baloldali perem), vagy
(baloldali perem), vagy 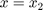 (jobboldali perem).
(jobboldali perem).
Az itt szereplő 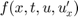 -t már a PDE egyenletének
megadása során meghatároztuk:
-t már a PDE egyenletének
megadása során meghatároztuk:  .
.
Cél: 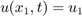 és
és 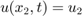 , ahol
, ahol 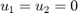 , ezért
, ezért
![$$ \left\{ \begin{array}{ll} p_1(x_1,t,u(x_1,t)) = u(x_1,t) - u_1, & q_1(x_1,t) = 0 \\[10pt] p_2(x_2,t,u(x_2,t)) = u(x_2,t) - u_2, & q_1(x_1,t) = 0 \end{array} \qquad \forall t > t_0 \right. $$](pde_heat_transfer_finite_triangle_eq08063338971970317067.png)
u1 = 0;
u2 = 0;
% Boundary conditions
bc = @(x1,u_x1,x2,u_x2,t) deal( u_x1 - u1, 0, u_x2 - u2, 0 );
A bc egy olyan anoním függvény
kell legyen, ami öt argumentumot vár: 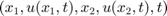 és
négy visszatérési értéke
van. Az első kettő a baloldali peremfeltételre
vonatkozó
és
négy visszatérési értéke
van. Az első kettő a baloldali peremfeltételre
vonatkozó 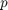 és
és 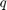 függvények, a második kettő
pedig a jobboldalra vonatkozó peremfeltétel
függvények, a második kettő
pedig a jobboldalra vonatkozó peremfeltétel
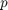 és
és 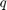 függvényei.
függvényei.
Lehet próbálkozni különböző peremfeltételekkel is:
% Izolált rendszer (a végeken nincs hőveszteség) bc = @(x1,u_x1,x2,u_x2,t) deal( 0, 1, 0, 1 ); % Mindkét végét melegítjük % bc = @(x1,u_x1,x2,u_x2,t) deal( u_x1 - 0.1, 0, u_x2 - 0.9, 0 ); % Mindkét végét melegítjük (de a melegítés exponenciálisan lecseng) % bc = @(x1,u_x1,x2,u_x2,t) deal( u_x1 - exp(-10*t), 0, u_x2 - exp(-10*t), 0 );
Numerikus megoldás pdepe segítségével
m = 0; x = linspace(0,1,101); t = linspace(0,0.1,101); sol = pdepe(m,pde,ic,bc,x,t);
Vizualizáció
% Ha netán több megoldása lenne (ezzel még nem volt baj), akkor az % első legyen az amit kiplottolunk. u = sol(:,:,1); fig = figure('Position', [165 540 1066 380], 'Color', 'white'); subplot(121), surf(x,t,u), light, shading interp xlabel('Distance x') ylabel('Time t') clear frames subplot(122), for i = 1:numel(t) plot(x, u(i,:)); title(sprintf('time = %0.3f, $\\int u(x,t)\\rm{d}x = %0.5f$', t(i), trapz(x, u(i,:))), 'Interpreter', 'latex'), axis([0, 1, 0, 1]) pause(0.1), if i == 10 persist.pub_vid_poster('hovez_veges_haromszog') end frames(i) = getframe(fig); end persist.pub_vid_write(frames)