Ezt a példát a MathWorks oldaláról töltöttem le és írtam át demonstráció végett.
This example shows how to solve a nonlinear elliptic problem numerically, using the pdenonlin function in Partial Differential Equation Toolbox™. In many problems, the coefficients not only depend on spatial coordinates, but also on the solution itself. In toolbox wording, this kind of problem is called nonlinear. An example of this is the minimal surface equation.
We envision to minimize the surface of a two-variable function $u:S \to \mathbf{R}$, namely $$ I(u) = \iint_S ~~ \underbrace{ \sqrt{1 + (u'_x)^2 + (u'_y)^2} }_{F(\not x, \not u, u'_x, u'_y)} ~~ \mathrm{d}(x,y) \to \mathrm{min} $$ The Euler-Lagrange equation will look like: $$ \frac{\partial}{\partial x} \left( \frac{\partial F}{\partial u'_x} \right) + \frac{\partial}{\partial y} \left( \frac{\partial F}{\partial u'_y} \right) = \frac{\partial}{\partial x} \left( \frac{u'_x}{\sqrt{1 + (u'_x)^2 + (u'_y)^2}} \right) + \frac{\partial}{\partial y} \left( \frac{u'_y}{\sqrt{1 + (u'_x)^2 + (u'_y)^2}} \right) = 0 $$ We can reformulate the equation as follows: $$-\nabla \cdot \left( \frac{1}{\sqrt{1 + \left|\nabla u\right|^2}} \nabla u \right) = 0$$ We solve this equation on the unit disk, with $u(x,y) = \sin(3x)\cos(3y)$ for all $(x,y) \in \partial S$ boundary condition. The PDE coefficient c is the multiplier of $\nabla u$, namely $$\frac{1}{\sqrt{1 + \left|\nabla u\right|^2}}$$ c is a function of the solution $u$, so the problem is nonlinear.
Contents
Problem Definition
The following variables define the problem:
information, see the documentation page for circleg and pdegeom. * c, a, f: The coefficients of the PDE. Note that c is a character array. For more information on passing coefficients into pdenonlin, see the documentation page for assempde. * rtol: Tolerance for nonlinear solver.
c = '1./sqrt(1+ux.^2+uy.^2)';
a = 0;
f = 0;
rtol = 1e-3;
Geommetry
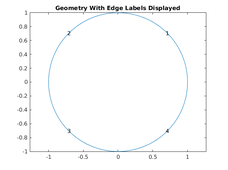
% Create a PDE Model with a single dependent variable numberOfPDE = 1; pdem = createpde(numberOfPDE); % Create a geometry entity and append to the pde model pdeGeom = @circleg; geometryFromEdges(pdem,pdeGeom); % Plot the geometry and display the edge labels for use in the boundary condition definition. figure; pdegplot(pdem, 'edgeLabels', 'on'); axis equal title 'Geometry With Edge Labels Displayed';
Boundary Conditions
bc_fh = @(x,y) sin(3*x).*cos(3*y); bcFunc = @(thePde, loc, state) bc_fh(loc.x,loc.y); applyBoundaryCondition(pdem,'Edge',(1:4), 'u', bcFunc);
Generate Mesh
msh = generateMesh(pdem,'Hmax',0.02); figure; pdemesh(pdem); axis equal
Solve PDE
Because the problem is nonlinear, we solve it using the pdenonlin function.
u = pdenonlin(pdem,c,a,f,'tol',rtol, 'Jacobian', 'full', 'Report', 'on');
Iteration Residual Step size Jacobian: full 0 3.6280e-02 1 3.0928e-03 1.0000000 2 3.3439e-04 1.0000000
Plot Solution
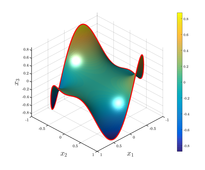
% Ennek segitsegevel lehet visszakerni a celtartomany hatarainak koordinatait figure, h = pdegplot(pdeGeom); x1 = h.XData; x2 = h.YData; delete(h), close; % Koordinata rendszer kialakitasa, stb... fig = figure('InvertHardcopy','off','Color',[1 1 1], ... 'Units', 'normalized', 'Position', [0 0 0.6 1]); ax = axes('Parent',fig,'LineWidth',2,'FontSize',16,... 'FontName','TeX Gyre Schola Math',... 'DataAspectRatio',[1 1 1]); hold(ax, 'on'); axis(ax, 'tight'); colorbar, light('Parent', ax) view(ax,[135,32]); grid(ax,'on'); xlabel('$x_1$','FontSize',30,'Interpreter','latex'); ylabel('$x_2$','FontSize',30,'Interpreter','latex'); zlabel('$x_3$','FontSize',30,'Interpreter','latex'); % Felulet kirajzolasa trisurf(msh.Elements', msh.Nodes(1,:)', msh.Nodes(2,:)', u, 'facealpha', 1); shading interp % Drotkeret kirajzolasa plot3(x1,x2,bc_fh(x1,x2), 'r', 'LineWidth', 4)