file:   anal3_1het.m
author: Polcz Péter <ppolcz@gmail.com>
Created on 2016.09.14. Wednesday, 16:35:09

Contents

Segédfüggvények létrehozása

A vektoranalízishez kapcsolódó segédfüggvények: vekanal_... megtalálható a demonstrációk repository-ban, a lib/matlab mappában: https://github.com/ppolcz/demonstrations/tree/master/lib/matlab

Utólag rádöbbentem, hogy teljesen fölösleges ezeket létrehozni, inkább használkuk a beépített `curl`, `divergence`, `gradient`, `jacobian`, `hessian`, `laplacian`, stb... függvényeket

MathWorks - Vector Analysis

web(fullfile(docroot, 'symbolic/vector-analysis.html'))

div = @vekanal_div;
rot = @vekanal_rot;
cross = @vekanal_cross;

divergencia demo

syms x y z real
r = [x;y];

F = [
    x^2*y
    y*x
    ];

F = [
    sin(x)
    cos(y)
    ];

divF = divergence(F,r);

[xx,yy] = ndgrid(linspace(-4,4,30));
rr = {xx,yy};

divF_num = vekanal_subsmesh(divF, r, rr);
[F1,F2] = vekanal_subsmeshn(F, r, rr);

figure, hold on, axis tight
quiver3(xx,yy,divF_num,F1,F2,F2*0,1.5),
surf(xx,yy,divF_num,'facealpha', 0.5),
shading interp
colorbar
title(sprintf('$F = %s, ~~ \\nabla F = %s$', latex(F'), latex(divF)), 'interpreter', 'latex')

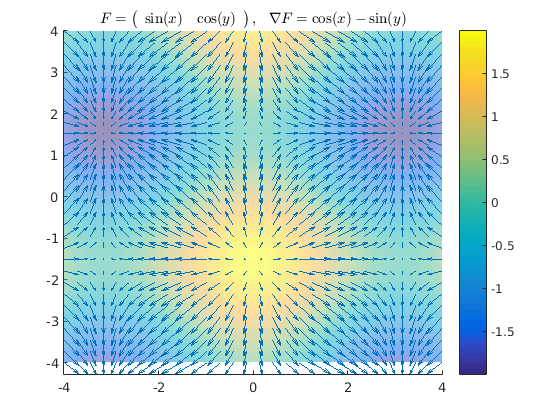
2. és 3. feladat

syms x y z real
r = [x;y;z];

% 2. feladat függvénye
F = [
    y/z
    z/x
    x/y
    ];

% 3. feladat függvénye
F = [
    x^2*y
    y*z
    x*y*z^2
    ];

divergence(F,r)
curl(F,r)

n = 20;
[xx,yy,zz] = ndgrid(linspace(-1,1,n));
rr = {xx,yy,zz};

[F1,F2,F3] = vekanal_subsmeshn(F, r, rr);

figure,
quiver3(xx,yy,zz,F1,F2,F3), axis equal tight

 
ans =
 
z + 2*x*y + 2*x*y*z
 
 
ans =
 
 x*z^2 - y
    -y*z^2
      -x^2

4. feladat

% Először deklaráljuk a szimbólikus objektumokat
syms x y z
r = [x;y;z];

f = sym('f(x,y,z)');
g = sym('g(x,y,z)');

F = [
    sym('F1(x,y,z)')
    sym('F2(x,y,z)')
    sym('F3(x,y,z)')
    ];

G = [
    sym('G1(x,y,z)')
    sym('G2(x,y,z)')
    sym('G3(x,y,z)')
    ];

% Feltételezzük, hogy minden szimbólikus objektum valós (nem komplex)
assume([F,G,f,g,r],'real')

% Gradiens, divergencia, rotáció, vektoriális szorzat műveletek
grad = @(f) jacobian(f,r);
trans = @(F) reshape(F,[1 3]);

% Végül a szabályok ellenőrzése, nullát kell kapjunk minden esetben
simplify(grad(f*g) - (f*grad(g) + g*grad(f)))
simplify(div(f*F) - (grad(f)*F + f*div(F)))
simplify(rot(f*F) - (cross(grad(f),F) + f*rot(F)))
simplify(div(cross(F,G)) - (trans(G)*rot(F) - trans(F)*rot(G)))

% 5. szabaly (nincs a feladatok kozott)
simplify(grad(trans(F)*G) - trans(F)*grad(G) - trans(G)*grad(F))

 
ans =
 
[ 0, 0, 0]
 
 
ans =
 
0
 
 
ans =
 
 0
 0
 0
 
 
ans =
 
0
 
 
ans =
 
[ 0, 0, 0]

5. feladat

Integráljuk az $F(x,y) = \left( x^2, \-y^2 \right)$ vektormezőt a $\Gamma$ negyed-ellipszis mentén. Az ellipszis origó középpontú, tengelyeinek hossza $2a$ és $2b$. Kezdőpont $A(a,0)$, végpont $B(0,b)$

syms t x y a b real
r = [x;y];

% Az ellipszis átmérői
% a = 2;
% b = 1;

% F(x,y) = F(r) kétdimenziós vektormező
F = [
    x^2
    y^2
    ];

% g, mint gamma paraméteres megadású függvény
g = [
    a*cos(t)
    b*sin(t)
    ];

% Integrálási tartomány:
t1 = 0;
t2 = pi/2;

% r = [x;y] helyére behelyettesítjük g deriváltját
Integrand = subs(F,r,g)' * diff(g, t);
pretty(Integrand)

% symbolikus integralassal:
Integral = int(Integrand, t);
I = subs(Integral,t,t2) - subs(Integral,t,t1);

disp 'Az integral erteke:'
pretty(I)

 3              2    3       2
b  cos(t) sin(t)  - a  cos(t)  sin(t)

Az integral erteke:
 3    3
b    a
-- - --
 3    3

6. feladat

syms t x y z real
r = [x;y;z];

% F(x,y) = F(r) háromdimenziós vektormező
F = [
    3*x^2*y^2*z
    2*x^3*y*z
    x^3*y^2
    ];

% g, mint gamma paraméteres megadású függvény
g = t * [1;2;3];

% Integrálási tartomány:
t1 = 0;
t2 = 1;

% r = [x;y;z] helyére behelyettesítjük g deriváltját
Integrand = subs(F,r,g)' * diff(g, t);

disp 'Integralando fuggveny tehat'
pretty(Integrand)

disp 'Szimmbolikus integralassal:'
disp 'Határozatlan:'
Integral = int(Integrand, t);
pretty(Integral)

disp 'Határozott:'
Integral = int(Integrand, t, t1, t2);
disp(Integral)

disp 'Polinomkozeliteses numerikus eljarassal:'
Integrand_fh = matlabFunction(Integrand);
Integral = integral(Integrand_fh, t1, t2);
disp(Integral)

Integralando fuggveny tehat
    5
72 t

Szimmbolikus integralassal:
Határozatlan:
    6
12 t

Határozott:
12
 
Polinomkozeliteses numerikus eljarassal:
    12


Published with MATLAB® R2015a