Tartalomjegyzék

ccs_nonline_Polcz_Ex1a_feedbacklin

Teljes Matlab script kiegészítő függvényekkel.

File: ccs_nonline_Polcz_Ex1a_feedbacklin.m
Directory: 4_gyujtemegy/11_CCS/_2_nonlin-pannon/2018
Author: Peter Polcz (ppolcz@gmail.com)

Created on 2018. August 13.

Model description

syms t u v real
syms x1 x2 x3 real
syms z1 z2 z3 real

x = [x1 ; x2 ; x3];
z = [z1 ; z2 ; z3];

d = @(g) jacobian(g,x);
Lie = @(f,g) d(g)*f;
br = @(f,g) d(g)*f - d(f)*g;

f = [
    x3*sin(x1)
    x3 - x3*x2*cos(x1)
    x1 + x2
    ];

g = [
    0
    1
    sin(x1)
    ];

h = x1 + x3 - x2*sin(x1);

phi3 = x3 - x2*sin(x1);

Phi = [
    h
    Lie(f,h)
    phi3
    ];

% Quick check: should be zero
% Lie(g,phi3)

\begin{align}\Phi(x) = \left(\begin{array}{c} x_{1}+x_{3}-x_{2}\,\sin\left(x_{1}\right)\\ x_{1}+x_{2}-\sin\left(x_{1}\right)\,\left(x_{3}-x_{2}\,x_{3}\,\cos\left(x_{1}\right)\right)-x_{3}\,\sin\left(x_{1}\right)\,\left(x_{2}\,\cos\left(x_{1}\right)-1\right)\\ x_{3}-x_{2}\,\sin\left(x_{1}\right) \end{array}\right)\end{align}

Quick check

\begin{align}L_g \phi_3(x) = 0\end{align}

$\phi_3(x)$ is given by Isidori, but anyone can check that this is indeed a solution for the PDE. This solution can also be computed by Mathematica.

Phi_inv = struct2cell(solve(z-Phi, x1, x2, x3));
Phi_inv = [ Phi_inv{:} ]';

\begin{align}\Phi^{-1}(z) = \left(\begin{array}{c} z_{1}-z_{3}\\ z_{2}-z_{1}+z_{3}\\ z_{3}+\sin\left(z_{1}-z_{3}\right)\,\left(z_{2}-z_{1}+z_{3}\right) \end{array}\right)\end{align}

Coordinate transformation

b = simplify(Lie(f, Lie(f,h)));
a = simplify(Lie(g, Lie(f,h)));
q3 = simplify(Lie(f, Phi(3)));

\begin{align}b(x) = x_{3}\,\left(\sin\left(x_{1}\right)-x_{2}\,\cos\left(x_{1}\right)+1\right),~ a(x) = 1,~ q_3(x) = x_{1}+x_{2}-x_{3}\,\sin\left(x_{1}\right)\end{align}

b = simplify(subs(b, x, Phi_inv));
a = simplify(subs(a, x, Phi_inv));
q3 = simplify(subs(q3, x, Phi_inv));

\begin{align}b(z) = \left(z_{3}+\sin\left(z_{1}-z_{3}\right)\,\left(z_{2}-z_{1}+z_{3}\right)\right)\,\left(\sin\left(z_{1}-z_{3}\right)-\cos\left(z_{1}-z_{3}\right)\,\left(z_{2}-z_{1}+z_{3}\right)+1\right),~ a(z) = 1,~ q_3(z) = z_{2}-\sin\left(z_{1}-z_{3}\right)\,\left(z_{3}+\sin\left(z_{1}-z_{3}\right)\,\left(z_{2}-z_{1}+z_{3}\right)\right)\end{align}

dz = simplify([ z2 ; collect(b+a*u,u) ; q3 ]);

System dynamics in the new coordinates

\begin{align}\dot z = \left(\begin{array}{c} z_{2}\\ u+\left(z_{3}+\sin\left(z_{1}-z_{3}\right)\,\left(z_{2}-z_{1}+z_{3}\right)\right)\,\left(\sin\left(z_{1}-z_{3}\right)-\cos\left(z_{1}-z_{3}\right)\,\left(z_{2}-z_{1}+z_{3}\right)+1\right)\\ z_{2}-\sin\left(z_{1}-z_{3}\right)\,\left(z_{3}+\sin\left(z_{1}-z_{3}\right)\,\left(z_{2}-z_{1}+z_{3}\right)\right) \end{array}\right)\end{align}

Linearizing feedback design

u_fdb = a \ (-b + v);

\begin{align}u = v-\left(z_{3}+\sin\left(z_{1}-z_{3}\right)\,\left(z_{2}-z_{1}+z_{3}\right)\right)\,\left(\sin\left(z_{1}-z_{3}\right)-\cos\left(z_{1}-z_{3}\right)\,\left(z_{2}-z_{1}+z_{3}\right)+1\right)\end{align}

Closed loop

dz_fdb = simplify(subs(dz, u, u_fdb));

\begin{align}\dot z = \left(\begin{array}{c} z_{2}\\ v\\ z_{2}-\sin\left(z_{1}-z_{3}\right)\,\left(z_{3}+\sin\left(z_{1}-z_{3}\right)\,\left(z_{2}-z_{1}+z_{3}\right)\right) \end{array}\right)\end{align}

Zero dynamics

Zero_dynamics = simplify(subs(dz_fdb, [z1 z2 v], [0 0 0]));

The zero dynamics is stable in the origin.

\begin{align}\dot z_3 = -z_{3}\,\sin\left(z_{3}\right)\,\left(\sin\left(z_{3}\right)-1\right)\end{align}

Linearized dynamics

Overall dynamics without the zero dynamics.

A = [
    0 1
    0 0
    ];

B = [
    0
    1
    ];

C = [ 1 0 ];

sys = ss(A,B,C,0);

s = tf('s');

H = tf(sys)

eps1 = 0.01;
eps2 = 0.01;

H_control = s^2/(eps1*s^2 + eps2*s + 1);

He = minreal(feedback(H*H_control,1))

[POLES, ZEROS] = pzmap(He)

Frequency domain controller for the integrator chain

Transfer function of the feedback controller $H(s) = \frac{s + 5}{\alpha s + 1}$.

Download model here: Isidori_Example414_PID.slx

EXTRACT-IO

pcz_print_model('Isidori_Example414_PID', 'simulate', true)

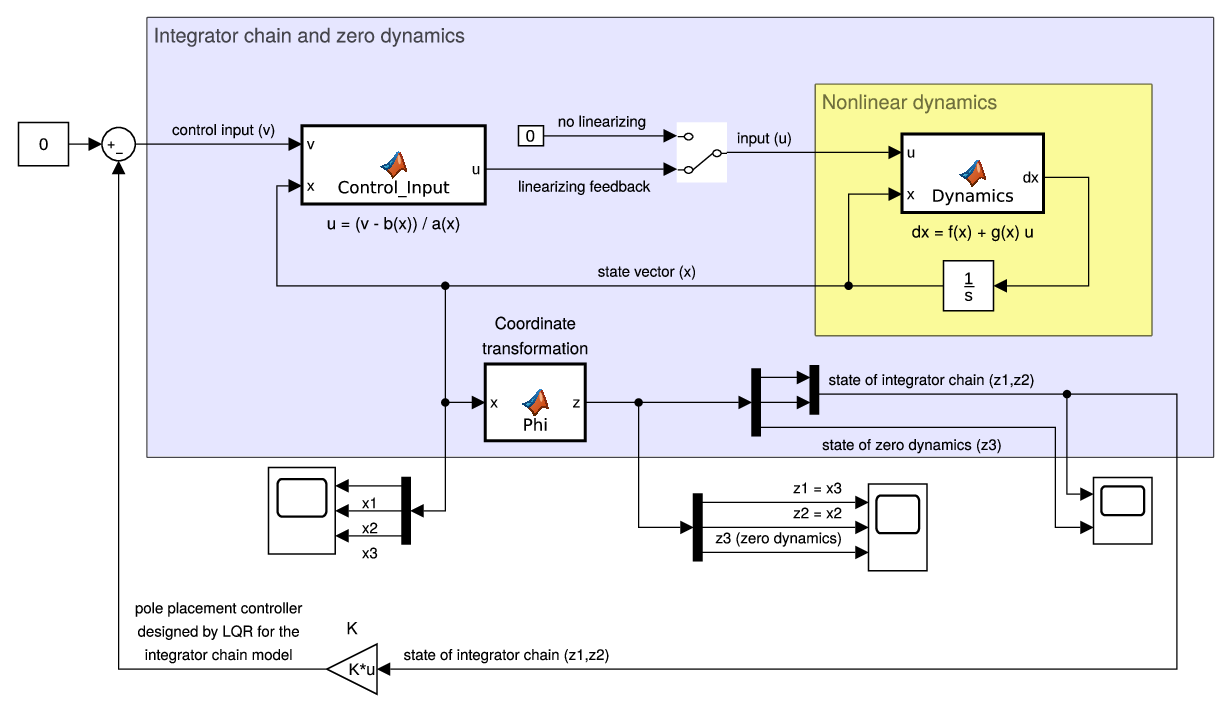
Pole placement controller

Download model here: Isidori_Example414_state_feedback.slx

% State feedback gain designed by LQR
K = lqr(A,B,0.1*eye(2),1);

EXTRACT-IO

pcz_print_model('Isidori_Example414_state_feedback', 'simulate', true)

Pole placement controller with observer (just for fun)

Note that when a linearizing feedback is applied, we need to know the full state vector. But we can play a little bit, what if we forget the values of the state variables.

Download model here: Isidori_Example414_obs_state_feedback.slx

% Observer for integrator chain
L = place(A',C',[-2 -3])';

% State feedback gain designed by LQR
K = lqr(A,B,0.1*eye(2),1);

EXTRACT-IO

pcz_print_model('Isidori_Example414_obs_state_feedback', 'simulate', true, 'density', 140)

Published with MATLAB® R2017b, and sanitarized by BeautifulSoup (Python script using BSoup is written by Polcz).