Tartalomjegyzék

Heat equation with ode45

Teljes Matlab script kiegészítő függvényekkel.

Approximate solution of the heat equation with |ode45| by considering the discretization along the spacial coordinate.

File: ccs_TG_hovezetes_PDE_megoldas_ode45.m
Directory: 4_gyujtemegy/11_CCS/_1_ccs/dynamic_system_simulations
Author: Peter Polcz (ppolcz@gmail.com)

Created on 2018. September 17.

Heat equation with a simple initial condition

$u'_t = k u''_{xx}$, where $k=1$. Initial condition: $u(x,0) = 1;

Let me discretize this equation about the spatial parameter $x$:

$$u''_{xx}[k] \simeq \frac{u[k+1] - 2 u[k] + u[k-1]}{(\Delta x)^2}$$

Therefore the PDE can be approximated by the following finite number of ordinary differential equations:

$$\pmqty{u'_t[0] \\ ... \\ u'_t[N-1]} = \pmqty{ -2 & 1 & 0 & ... & 0 \\ 1 & -2 & 1 & ... & 0 \\ ... & ... & ... & ... & ... \\ 0 & ... & 0 & -2 & 1 } \pmqty{u[0] \\ ... \\ u[N-1]}$$

Let the state vector $x$ be:

$$x = \pmqty{u[0] \\ ... \\ u[N-1]}, ~~\text{ and }~~ A = \pmqty{ -2 & 1 & 0 & ... & 0 \\ 1 & -2 & 1 & ... & 0 \\ ... & ... & ... & ... & ... \\ 0 & ... & 0 & -2 & 1 }$$

Then we have a linear autonomous system of ODEs: $\dot x = A x$. Note that matrix $A$ is a Toeplitz matrix due to its special diagonal structure.

% Nr of sample points;
N = 15;

% L = 10 meters long;
L = 10;

Dx = L / (N-1);

A = toeplitz([-2 1 zeros(1,N-2)]) / Dx^2;
B = [1 0 ; zeros(N-2,2) ; 0 1];
C = eye(N);
Cn = ctrb(A,B);
rankCn = rank(Cn)

f = @(t,x) A*x;

[t,y] = ode45(f, linspace(0,30,70), ones(N,1));

figure, surf(y)

Output:

rankCn =
    15

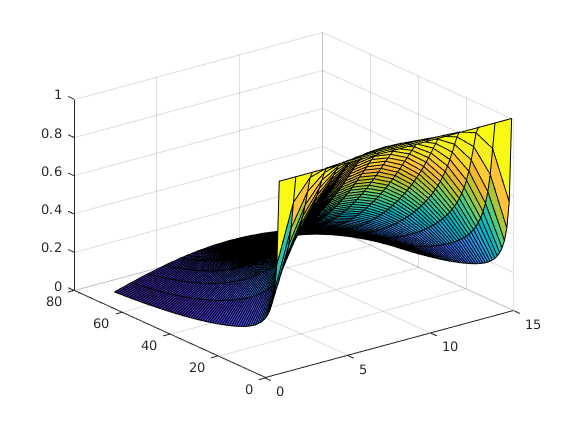
Controlled heat equation

K = lqr(A,B,10*eye(N),eye(2));

f = @(t,x) (A-B*K)*x;

[t,y] = ode45(f, linspace(0,30,70), ones(N,1));

figure, surf(y)

Published with MATLAB® R2017b, and sanitarized by BeautifulSoup (Python script using BSoup is written by Polcz).