Tartalomjegyzék
\[ \newenvironment{dcases}{\left\{\begin{array}{ll}}{\end{array}\right.} \]LPV system computations
Teljes Matlab script kiegészítő függvényekkel.
File: LPV_ctrb_obsv.m Directory: 2_demonstrations/workspace/ccs/ccs_2018 Author: Peter Polcz (ppolcz@gmail.com)
Created on 2018. October 09.
Define a very nice affine LPV system
A0 = [
1 3
0 -3
];
A1 = [
0 -1
0 1
];
A2 = [
0 0.5
0 0
];
B0 = [
1
0
];
B1 = [
0.5
0
];
B2 = [
0.1
0
];
C = [ 1 0 ];
D = 0;
% n: number of states, n = dim(x)
% m: number of inputs, m = dim(u)
% p: number of outputs, p = dim(y)
% r: number of uncertain parameters, r = dim(rho)
[n,m] = size(B0);
p = size(C,1);
r = 2;
A_fh = @(rho) A0 + rho(1)*A1 + rho(2)*A2;
B_fh = @(rho) B0 + rho(1)*B1 + rho(2)*B2;
rho1_lim = [-1 1];
rho2_lim = [-2 2];
rho_lim = [
rho1_lim
rho2_lim
];
rho_lims_cell = num2cell(rho_lim,2);
X = allcomb(rho_lims_cell{:});
Quadratic detectability
Using linear matrix inequalities, try to find an observer gain $L$, such that the observer's dynamics is $\dot {\hat x} = A(\varrho) \hat x + B u + L(y - \hat y)$, and the error dynamics $\dot e = \dot x - \dot {\hat x} = (A(\varrho) - L C) e$ is asymptotically stable by the means of a quadratic Lyapunov function $V(x) = x^T P x$ for any admissible parameter value.
M = sdpvar(n,p,'full');
P = sdpvar(n);
CONS = [ P - 0.001*eye(n) >= 0 ];
for i = 1:size(X,1)
rhoi = X(i,:)';
Ai = A_fh(rhoi);
CONS = [ CONS
Ai'*P + P*Ai - M*C - C'*M' + 0.001*eye(n) <= 0
];
end
sdpopts = sdpsettings('solver', 'sedumi');
sol = optimize(CONS,[],sdpopts)
P = double(P);
M = double(M);
L = P\M;
Output:
SeDuMi 1.3 by AdvOL, 2005-2008 and Jos F. Sturm, 1998-2003.
Alg = 2: xz-corrector, theta = 0.250, beta = 0.500
eqs m = 5, order n = 11, dim = 21, blocks = 6
nnz(A) = 31 + 0, nnz(ADA) = 25, nnz(L) = 15
it : b*y gap delta rate t/tP* t/tD* feas cg cg prec
0 : 2.55E+02 0.000
1 : 0.00E+00 5.50E+01 0.000 0.2158 0.9000 0.9000 1.00 1 1 1.1E+01
2 : 0.00E+00 3.46E+00 0.000 0.0629 0.9900 0.9900 1.00 1 1 7.1E-01
3 : 0.00E+00 1.79E-03 0.000 0.0005 0.9999 0.9999 1.00 1 1 3.7E-04
4 : 0.00E+00 1.79E-10 0.000 0.0000 1.0000 1.0000 1.00 1 1 3.7E-11
iter seconds digits c*x b*y
4 0.0 3.9 -1.2725285253e-14 0.0000000000e+00
|Ax-b| = 2.6e-11, [Ay-c]_+ = 0.0E+00, |x|= 8.1e-12, |y|= 1.1e+00
Detailed timing (sec)
Pre IPM Post
1.336E-02 2.036E-02 3.772E-03
Max-norms: ||b||=0, ||c|| = 1.000000e-03,
Cholesky |add|=0, |skip| = 0, ||L.L|| = 3.06178.
sol =
struct with fields:
yalmiptime: 0.1889
solvertime: 0.0380
info: 'Successfully solved (SeDuMi-1.3)'
problem: 0
Check solution
for i = 1:size(X,1)
rhoi = X(i,:)';
Ai = A_fh(rhoi);
eig(Ai - L*C)
end
Output:
ans = -2.8427 + 1.3507i -2.8427 - 1.3507i ans = -2.8427 + 1.9833i -2.8427 - 1.9833i ans = -1.8427 + 1.0148i -1.8427 - 1.0148i ans = -1.8427 + 1.7717i -1.8427 - 1.7717i
Estimate L2 norm
Compute the induced $\mathcal L_2$ operator gain for system $(A(\varrho) - B(\varrho) K, B(\varrho), C)$, where $K = (5 , 5)$ is a robust stabilising static state feedback gain.
K = [5 5];
P = sdpvar(n);
gammaSqr = sdpvar;
CONS = [ P - 0.001*eye(n) >= 0, gammaSqr >= 0 ];
for i = 1:size(X,1)
rhoi = X(i,:)';
Ai = A_fh(rhoi);
Bi = B_fh(rhoi);
Ak = Ai - Bi*K;
eig(Ak)
Lambda = [
Ak'*P + P*Ak + C'*C , P * Bi
Bi'*P , -eye(m)*gammaSqr
];
CONS = [ CONS
Lambda <= 0
];
end
sdpopts = sdpsettings('solver', 'sedumi');
sol = optimize(CONS,gammaSqr,sdpopts)
% Check LMI solution
check(CONS)
gammaSqr = double(gammaSqr);
gamma = sqrt(gammaSqr)
Output:
ans =
-0.5000
-4.0000
ans =
-2.5000
-4.0000
ans =
-5.5000
-2.0000
ans =
-7.5000
-2.0000
SeDuMi 1.3 by AdvOL, 2005-2008 and Jos F. Sturm, 1998-2003.
Alg = 2: xz-corrector, theta = 0.250, beta = 0.500
eqs m = 4, order n = 16, dim = 42, blocks = 6
nnz(A) = 36 + 0, nnz(ADA) = 16, nnz(L) = 10
it : b*y gap delta rate t/tP* t/tD* feas cg cg prec
0 : 7.44E+01 0.000
1 : -3.24E+00 1.72E+01 0.000 0.2306 0.9000 0.9000 -0.30 1 1 3.6E+01
2 : -5.60E+00 5.04E+00 0.000 0.2937 0.9000 0.9000 0.12 1 1 1.7E+01
3 : -3.37E+00 1.32E+00 0.000 0.2628 0.9000 0.9000 0.80 1 1 4.1E+00
4 : -9.84E-01 2.83E-01 0.000 0.2139 0.9000 0.9000 1.31 1 1 7.6E-01
5 : -5.43E-01 7.11E-02 0.000 0.2512 0.9000 0.9000 0.88 1 1 2.1E-01
6 : -4.25E-01 2.08E-02 0.000 0.2920 0.9000 0.9000 0.70 1 1 7.4E-02
7 : -3.95E-01 6.27E-03 0.000 0.3021 0.9000 0.9000 0.68 1 1 2.6E-02
8 : -3.76E-01 1.43E-03 0.000 0.2276 0.9000 0.9000 0.66 1 1 7.4E-03
9 : -3.71E-01 4.18E-04 0.000 0.2926 0.9000 0.9000 0.62 1 1 2.7E-03
10 : -3.68E-01 1.34E-04 0.000 0.3214 0.9000 0.9000 0.56 1 1 1.1E-03
11 : -3.67E-01 4.58E-05 0.000 0.3410 0.9000 0.9000 0.57 1 1 4.9E-04
12 : -3.66E-01 1.75E-05 0.000 0.3815 0.9000 0.9000 0.60 1 1 2.4E-04
13 : -3.65E-01 6.79E-06 0.000 0.3885 0.9000 0.9000 0.62 1 1 1.2E-04
14 : -3.65E-01 3.30E-06 0.000 0.4867 0.9000 0.9000 0.58 1 1 7.4E-05
15 : -3.65E-01 1.41E-06 0.000 0.4264 0.9000 0.9000 0.66 1 1 3.7E-05
16 : -3.64E-01 7.02E-07 0.000 0.4988 0.9000 0.9000 0.44 1 1 2.6E-05
17 : -3.64E-01 2.61E-07 0.000 0.3717 0.9000 0.9000 0.62 1 1 1.2E-05
18 : -3.64E-01 1.11E-07 0.000 0.4254 0.9000 0.9000 0.46 1 1 7.1E-06
19 : -3.64E-01 4.25E-08 0.000 0.3822 0.9000 0.9000 0.57 1 1 3.4E-06
20 : -3.64E-01 1.91E-08 0.000 0.4507 0.9000 0.9000 0.42 1 1 2.2E-06
21 : -3.64E-01 7.19E-09 0.000 0.3756 0.9000 0.9000 0.57 2 2 1.0E-06
22 : -3.64E-01 3.13E-09 0.000 0.4358 0.9000 0.9000 0.42 2 2 6.5E-07
23 : -3.64E-01 1.18E-09 0.000 0.3773 0.9000 0.9000 0.56 3 3 3.1E-07
24 : -3.64E-01 5.23E-10 0.000 0.4424 0.9000 0.9000 0.41 3 3 2.0E-07
25 : -3.64E-01 1.97E-10 0.000 0.3760 0.9000 0.9000 0.56 3 3 9.3E-08
26 : -3.64E-01 8.65E-11 0.000 0.4401 0.9000 0.9000 0.41 3 3 5.9E-08
27 : -3.64E-01 3.25E-11 0.000 0.3761 0.9000 0.9000 0.55 3 3 2.8E-08
28 : -3.64E-01 1.43E-11 0.000 0.4410 0.9000 0.9000 0.41 3 3 1.8E-08
29 : -3.64E-01 5.39E-12 0.000 0.3759 0.9000 0.9000 0.55 3 3 8.4E-09
30 : -3.64E-01 2.38E-12 0.000 0.4405 0.9000 0.9000 0.41 3 3 5.4E-09
31 : -3.64E-01 8.93E-13 0.000 0.3758 0.9000 0.9000 0.55 3 3 2.5E-09
32 : -3.64E-01 3.93E-13 0.000 0.4406 0.9000 0.9000 0.41 3 3 1.6E-09
33 : -3.64E-01 1.48E-13 0.000 0.3758 0.9000 0.9000 0.55 3 3 7.6E-10
iter seconds digits c*x b*y
33 0.1 6.1 -3.6364097837e-01 -3.6364071889e-01
|Ax-b| = 9.9e-10, [Ay-c]_+ = 0.0E+00, |x|= 1.2e+00, |y|= 7.1e+03
Detailed timing (sec)
Pre IPM Post
2.877E-03 1.019E-01 5.633E-04
Max-norms: ||b||=1, ||c|| = 1,
Cholesky |add|=1, |skip| = 0, ||L.L|| = 640.087.
sol =
struct with fields:
yalmiptime: 0.1687
solvertime: 0.1055
info: 'Numerical problems (SeDuMi-1.3)'
problem: 4
post =
1×1 cell array
{'A primal-dual optimal solution would show non-negative residuals.'}
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
| ID| Constraint| Primal residual| Dual residual|
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
| #1| Matrix inequality| 1.817| 3.4655e-11|
| #2| Elementwise inequality| 0.36364| 7.1486e-07|
| #3| Matrix inequality| 2.2595e-07| 4.4019e-12|
| #4| Matrix inequality| 0.15942| 4.332e-12|
| #5| Matrix inequality| 0.068514| 8.6588e-12|
| #6| Matrix inequality| 5.9233e-07| 4.8625e-12|
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
| A primal-dual optimal solution would show non-negative residuals. |
| In practice, many solvers converge to slightly infeasible |
| solutions, which may cause some residuals to be negative. |
| It is up to the user to judge the importance and impact of |
| slightly negative residuals (i.e. infeasibilities) |
| https://yalmip.github.io/command/check/ |
| https://yalmip.github.io/faq/solutionviolated/ |
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
gamma =
0.6030
Minimize L2 norm
Compute the optimal feedback gain $K$, \mbox{$u = -K x + v$} (where $v$ is a disturbance input), that stabilizes the system and gives a minimal L2 gain from the disturbance $v$ to the output $y$.
N = sdpvar(m,n, 'full');
Q = sdpvar(n);
gammaSqr = sdpvar;
CONS = [ Q - 0.001*eye(n) >= 0, gammaSqr >= 0 ];
for i = 1:size(X,1)
rhoi = X(i,:)';
Ai = A_fh(rhoi);
Bi = B_fh(rhoi);
Lambda = [
Q*Ai' + Ai*Q - Bi*N - N'*Bi' , Bi , Q*C'
Bi' , -eye(m)*gammaSqr , zeros(m,p)
C*Q , zeros(p,m) , -eye(p)
];
CONS = [ CONS
Lambda <= 0
];
end
sdpopts = sdpsettings('solver', 'sedumi');
sol = optimize(CONS,gammaSqr,sdpopts)
check(CONS)
Q = double(Q);
N = double(N);
P = inv(Q);
K = N/Q;
gammaSqr = double(gammaSqr);
gamma = sqrt(gammaSqr)
Output:
SeDuMi 1.3 by AdvOL, 2005-2008 and Jos F. Sturm, 1998-2003.
Alg = 2: xz-corrector, theta = 0.250, beta = 0.500
eqs m = 6, order n = 20, dim = 70, blocks = 6
nnz(A) = 44 + 0, nnz(ADA) = 36, nnz(L) = 21
it : b*y gap delta rate t/tP* t/tD* feas cg cg prec
0 : 2.69E+01 0.000
1 : -1.43E+00 9.74E+00 0.000 0.3620 0.9000 0.9000 1.69 1 1 1.3E+01
2 : -8.17E-01 2.50E+00 0.000 0.2567 0.9000 0.9000 2.01 1 1 2.4E+00
3 : -4.43E-01 5.99E-01 0.000 0.2395 0.9000 0.9000 1.08 1 1 6.4E-01
4 : -2.69E-01 1.63E-01 0.000 0.2718 0.9000 0.9000 0.67 1 1 2.6E-01
5 : -1.48E-01 3.95E-02 0.000 0.2427 0.9000 0.9000 0.45 1 1 1.1E-01
6 : -9.28E-02 1.16E-02 0.000 0.2930 0.9000 0.9000 0.41 1 1 3.0E-02
7 : -6.04E-02 3.48E-03 0.000 0.3006 0.9000 0.9000 0.40 1 1 1.2E-02
8 : -4.15E-02 1.10E-03 0.000 0.3160 0.9000 0.9000 0.43 1 1 5.5E-03
9 : -2.87E-02 3.82E-04 0.000 0.3479 0.9000 0.9000 0.44 1 1 2.8E-03
10 : -2.19E-02 1.44E-04 0.000 0.3763 0.9000 0.9000 0.51 1 1 1.4E-03
11 : -1.42E-02 5.04E-05 0.000 0.3506 0.9000 0.9000 0.37 1 1 7.4E-04
12 : -1.12E-02 1.85E-05 0.000 0.3665 0.9000 0.9000 0.53 1 1 3.4E-04
13 : -7.24E-03 5.83E-06 0.000 0.3154 0.9000 0.9000 0.40 1 1 1.7E-04
14 : -5.41E-03 2.08E-06 0.000 0.3572 0.9000 0.9000 0.48 1 1 8.0E-05
15 : -3.43E-03 6.70E-07 0.000 0.3218 0.9000 0.9000 0.35 1 1 4.0E-05
16 : -2.61E-03 2.38E-07 0.000 0.3545 0.9000 0.9000 0.49 1 1 1.9E-05
17 : -1.68E-03 7.49E-08 0.000 0.3154 0.9000 0.9000 0.37 1 1 9.2E-06
18 : -1.26E-03 2.66E-08 0.000 0.3546 0.9000 0.9000 0.47 1 1 4.4E-06
19 : -8.08E-04 8.61E-09 0.000 0.3241 0.9000 0.9000 0.36 1 1 2.2E-06
20 : -6.14E-04 3.08E-09 0.000 0.3580 0.9000 0.9000 0.49 2 2 1.0E-06
21 : -3.95E-04 9.92E-10 0.000 0.3218 0.9000 0.9000 0.37 2 2 5.2E-07
22 : -2.99E-04 3.55E-10 0.000 0.3583 0.9000 0.9000 0.48 2 3 2.5E-07
23 : -1.92E-04 1.15E-10 0.000 0.3231 0.9000 0.9000 0.36 3 3 1.2E-07
24 : -1.46E-04 4.11E-11 0.000 0.3581 0.9000 0.9000 0.49 3 3 5.8E-08
25 : -9.38E-05 1.32E-11 0.000 0.3214 0.9000 0.9000 0.37 3 3 2.9E-08
26 : -7.10E-05 4.73E-12 0.000 0.3575 0.9000 0.9000 0.48 3 3 1.4E-08
27 : -4.56E-05 1.52E-12 0.000 0.3218 0.9000 0.9000 0.37 3 3 6.9E-09
28 : -3.45E-05 5.43E-13 0.000 0.3573 0.9000 0.9000 0.48 3 3 3.3E-09
29 : -2.22E-05 1.75E-13 0.000 0.3214 0.9000 0.9000 0.37 3 3 1.6E-09
30 : -1.68E-05 6.24E-14 0.000 0.3573 0.9000 0.9000 0.48 3 3 7.7E-10
iter seconds digits c*x b*y
30 0.2 1.2 -1.7821589180e-05 -1.6770683833e-05
|Ax-b| = 1.1e-09, [Ay-c]_+ = 0.0E+00, |x|= 7.1e-01, |y|= 5.5e+04
Detailed timing (sec)
Pre IPM Post
1.147E-03 8.775E-02 5.029E-04
Max-norms: ||b||=1, ||c|| = 3.400000e+00,
Cholesky |add|=1, |skip| = 0, ||L.L|| = 1.68909e+09.
sol =
struct with fields:
yalmiptime: 0.1492
solvertime: 0.0896
info: 'Numerical problems (SeDuMi-1.3)'
problem: 4
post =
1×1 cell array
{'A primal-dual optimal solution would show non-negative residuals.'}
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
| ID| Constraint| Primal residual| Dual residual|
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
| #1| Matrix inequality| 59.6435| 1.6192e-10|
| #2| Elementwise inequality| 1.6771e-05| 0.046714|
| #3| Matrix inequality| 1.318e-05| 1.6436e-11|
| #4| Matrix inequality| 9.0336e-06| 9.0071e-12|
| #5| Matrix inequality| 4.1868e-06| 4.2431e-12|
| #6| Matrix inequality| 7.3317e-07| 2.8045e-12|
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
| A primal-dual optimal solution would show non-negative residuals. |
| In practice, many solvers converge to slightly infeasible |
| solutions, which may cause some residuals to be negative. |
| It is up to the user to judge the importance and impact of |
| slightly negative residuals (i.e. infeasibilities) |
| https://yalmip.github.io/command/check/ |
| https://yalmip.github.io/faq/solutionviolated/ |
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
gamma =
0.0041
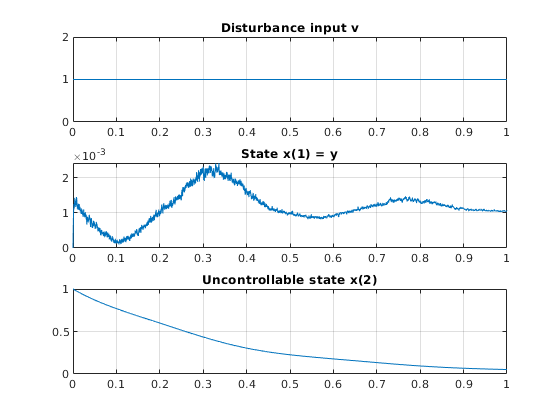
Check optimal L2 with simulation
rho = @(t) [
min(max(sin(14*t) + randn(size(t)) * rho1_lim(2),rho1_lim(1)),rho1_lim(2))
min(max(sin(41*t) + randn(size(t)) * rho2_lim(2),rho2_lim(1)),rho2_lim(2))
];
% v = @(t) sign(sin(31*t.^2));
v = @(t) ones(size(t));
f_ode = @(t,x) A_fh(rho(t))*x + B_fh(rho(t))*(-K*x + v(t));
[t,x] = ode45(f_ode, [0,1], [0;1]);
y = C*x';
figure
subplot(311), plot(t,v(t)), grid on, title 'Disturbance input v'
subplot(312), plot(t,x(:,1)), grid on, title 'State x(1) = y'
subplot(313), plot(t,x(:,2)), grid on, title 'Uncontrollable state x(2)'
L2_norm = @(t,u) sqrt( trapz(t,u.^2) );
L2_norm_of_v = L2_norm(t,v(t))
L2_norm_of_y = L2_norm(t,y)
Output_gain_for_this_input = L2_norm_of_y / L2_norm_of_v
return
Output:
L2_norm_of_v =
1
L2_norm_of_y =
0.0012
Output_gain_for_this_input =
0.0012
Using the Robust Control Toolbox
Unfortunatelly we do not have this toolbox yet.
d1 = ureal('d1', 0, 'Range', rho_lim(1,:));
d2 = ureal('d2', 0, 'Range', rho_lim(2,:));
A = [
2*d1 - 3, 0, 0, 0, 0
0, d1/2 - 1, 0, 0, 0
d2 - 2*d1 + 2, 0, d2 - 1, 0, 0
2 - d2, 0, 4 - 2*d1, 2*d1 + d2 - 5, 2*d1 - 4
d2 - 2*d1 + 2, 0, 0, 0, d2 - 1
];
B = [
-1
0
d2 - 2*d1 - 5
2*d2 - d1 - 2
- d1 - 2
];
C = [ -3 4 -2 2 4 ];
D = 0;
sys_unc = ss(A,B,C,D);
simplify(sys_unc,'full');
figure
bopts = bodeoptions;
bopts.MagUnits = 'abs';
% bodeplot(sys_unc,bopts), grid on;
bodeplot(gridureal(sys_unc,30), bopts), grid on
Nr_samples = 2500;
[peak_gain,freki] = getPeakGain(gridureal(sys_unc,Nr_samples));
[peak_gain,I] = max(peak_gain);
[wcg,wcu] = wcgain(sys_unc)
sys_fdb = ss(A-B*K,B,C,D);
simplify(sys_fdb,'full');
figure
bopts = bodeoptions;
bopts.MagUnits = 'abs';
% bodeplot(sys_unc,bopts), grid on;
bodeplot(gridureal(sys_fdb,30), bopts), grid on
Nr_samples = 2500;
[peak_gain,freki] = getPeakGain(gridureal(sys_fdb,Nr_samples));
[peak_gain,I] = max(peak_gain);
[wcg,wcu] = wcgain(sys_fdb)