Tartalomjegyzék
\[ \newenvironment{dcases}{\left\{\begin{array}{ll}}{\end{array}\right.} \]TELJES MATLAB SCRIPT KIEGÉSZÍTŐ FÜGGVÉNYEKKEL
file: vectorfield_Coulombs_law.m author: Polcz Péter <ppolcz@gmail.com>
Created on 2016.09.06. Tuesday, 10:56:21 Reviewed on 2017. August 25. [Vagó tanárnőnek képek generálása]
Output:
┌vectorfield_Coulombs_law │ - Persistence for `vectorfield_Coulombs_law` initialized [run ID: 3492, 2017.08.27. Sunday, 04:04:57] │ - Script `vectorfield_Coulombs_law` backuped
Pozitív és negatív ponttöltések töltések elektromos tere (normalizálva)
% Coulomb's constant
ke = 8.99e9;
e = -1.6e-19;
q = 10000 * e;
Qn = [ -2 -0.5 ];
Qp = [ 2 0.7 0.9 ];
rn = [
-5 0
0 9
];
rp = [
5 2 -8
0 -9 -8
];
Qs = [Qp Qn];
rs = [rp rn];
resolution = 20;
[x,y] = meshgrid(linspace(-10,10,resolution));
Fx = zeros(size(x));
Fy = Fx;
for i = 1:size(rs,2)
square_distance = (x-rs(1,i)).^2 + (y-rs(2,i)).^2;
Fx = Fx + ke * Qs(i) * q * (x - rs(1,i)) ./ (square_distance.^(3/2));
Fy = Fy + ke * Qs(i) * q * (y - rs(2,i)) ./ (square_distance.^(3/2));
end
Fr = (Fx.^2 + Fy.^2).^(1/2);
fig = figure('Units','normalized', 'Position', [0.3474 0.3611 0.4359 0.5389]);
hold on;
% quiver(x,y,Fx,Fy);
quiver(x,y,Fx./Fr,Fy./Fr,0.5);
s = {'' '' '+'};
R_divider = 3;
for i = 1:numel(Qs)
if Qs(i) > 0
color = 'r';
else
color = 'b';
end
R = abs(Qs(i))/R_divider;
rectangle('Position',[rs(1,i)-R,rs(2,i)-R,2*R,2*R],'Curvature',[1,1],...
'FaceColor',color,'EdgeColor',color);
end
axis equal tight
% title 'Normalized vector field between some electric point charge' interpreter latex
set(gca,'YTick',[-10 -5 0 5 10],'XTick',[-10 -5 0 5 10],persist.font.axis18{:});
plabel x '$x$'
plabel y '$y$'
set(get(gca,'ylabel'),'rotation',0)
% title 'Elektromos t\"{o}lt\''esek \''altal keltett (normaliz\''alt) elektromos t\''er' interpreter latex
% title 'Normalized vector field between some electric point charge' interpreter latex
% legend([h1 h2], {'negative','positive'},'Position',[0.85,0.8,0.1,0.1],'Box','off')
persist.png('ponttoltesek')
title 'T\"olt\''esek norm\''alt elektromos tere' interpreter latex
persist.png('ponttoltesek-szoveg')
Output:
│ - File saved to: /home/ppolcz/Repositories/Bitbucket/control-systems/zygote/dropbox_link/oktatas/anal3/1_vekanal/vectorfield_Coulombs_law/media/17_08_27_Time040457_runID3492_ponttoltesek.png │ - File saved to: /home/ppolcz/Repositories/Bitbucket/control-systems/zygote/dropbox_link/oktatas/anal3/1_vekanal/vectorfield_Coulombs_law/media/17_08_27_Time040457_runID3492_ponttoltesek-szoveg.png
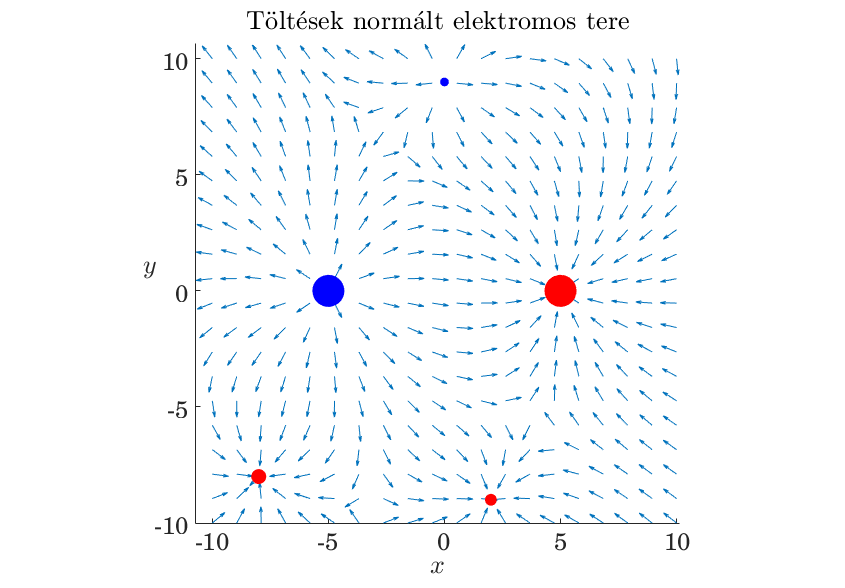
Ponttöltések elektromos tere véletlenszerű pontokban (normalizálva)
Reviewed on 2017.08.25. Friday, 14:35:51
% Coulomb's constant
ke = 8.99e9;
e = -1.6e-19;
Nr = 5;
q = 10000 * e;
Q = randn(1,Nr);
Q_pos = (rand(2,Nr)-0.5)*20;
[x,y] = meshgrid(linspace(min(min(min(Q_pos)),-10),max(max(max(Q_pos)),10),30));
Fx = zeros(size(x));
Fy = Fx;
for i = 1:size(Q_pos,2)
square_distance = (x-Q_pos(1,i)).^2 + (y-Q_pos(2,i)).^2;
Fx = Fx + ke * Q(i) * q * (x - Q_pos(1,i)) ./ (square_distance.^(3/2));
Fy = Fy + ke * Q(i) * q * (y - Q_pos(2,i)) ./ (square_distance.^(3/2));
end
Fr = (Fx.^2 + Fy.^2).^(1/2);
fig = figure('Units','normalized', 'Position', [0.3474 0.3611 0.4359 0.5389]);
% quiver(x,y,Fx,Fy);
quiver(x,y,Fx./Fr,Fy./Fr, 0.5), hold on;
for i = 1:size(Q_pos,2)
if Q(i) < 0
h1 = plot(Q_pos(1,i), Q_pos(2,i), '.r', 'linewidth', 10, 'markersize', 20);
else
h2 = plot(Q_pos(1,i), Q_pos(2,i), '.b', 'linewidth', 10, 'markersize', 20);
end
end
axis equal tight
set(gca,'YTick',[-10 -5 0 5 10],'XTick',[-10 -5 0 5 10],persist.font.axis18{:});
plabel x '$x$'
plabel y '$y$'
set(get(gca,'ylabel'),'rotation',0)
% title 'Elektromos t\"{o}lt\''esek \''altal keltett (normaliz\''alt) elektromos t\''er' interpreter latex
% title 'Normalized vector field between some electric point charge' interpreter latex
% legend([h1 h2], {'negative','positive'},'Position',[0.85,0.8,0.1,0.1],'Box','off')
persist.png('ponttoltesek')
title 'T\"olt\''esek norm\''alt elektromos tere' interpreter latex
persist.png('ponttoltesek-szoveg')
Output:
│ - File saved to: /home/ppolcz/Repositories/Bitbucket/control-systems/zygote/dropbox_link/oktatas/anal3/1_vekanal/vectorfield_Coulombs_law/media/17_08_27_Time040457_runID3492_ponttoltesek.png │ - File saved to: /home/ppolcz/Repositories/Bitbucket/control-systems/zygote/dropbox_link/oktatas/anal3/1_vekanal/vectorfield_Coulombs_law/media/17_08_27_Time040457_runID3492_ponttoltesek-szoveg.png

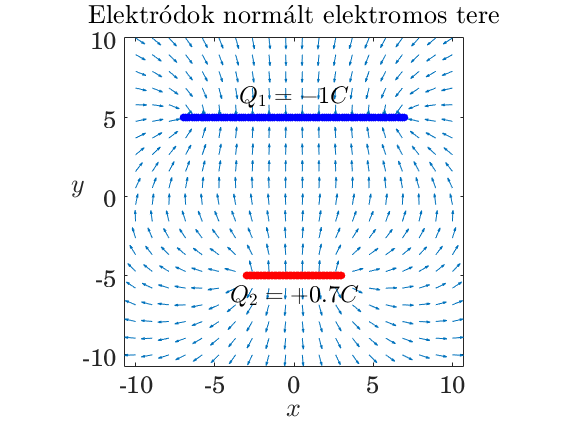
Anod és katód elektromos tere (ponttöltésekkel közelítve)
Reviewed on 2017.08.25. Friday, 14:36:01
% Coulomb's constant
ke = 8.99e9;
e = -1.6e-19;
q = 10000 * e;
Nr_anode = 100;
Nr_cathode = 70;
Q = [ 0.01*ones(1,Nr_anode) -0.01*ones(1,Nr_cathode) ];
Q_pos = [
linspace(-7,7,Nr_anode) linspace(-3,3,Nr_cathode)
5*ones(1,Nr_anode) -5*ones(1,Nr_cathode)
];
[x,y] = meshgrid(linspace(-10,10,20));
Fx = zeros(size(x));
Fy = Fx;
for i = 1:size(Q_pos,2)
square_distance = (x-Q_pos(1,i)).^2 + (y-Q_pos(2,i)).^2;
Fx = Fx + ke * Q(i) * q * (x - Q_pos(1,i)) ./ (square_distance.^(3/2));
Fy = Fy + ke * Q(i) * q * (y - Q_pos(2,i)) ./ (square_distance.^(3/2));
end
Fr = (Fx.^2 + Fy.^2).^(1/2);
fig = figure();
% quiver(x,y,Fx,Fy);
quiver(x,y,Fx./Fr,Fy./Fr, 0.5), hold on;
for i = 1:size(Q_pos,2)
if Q(i) < 0
h1 = plot(Q_pos(1,i), Q_pos(2,i), '.r', 'linewidth', 10, 'markersize', 20);
else
h2 = plot(Q_pos(1,i), Q_pos(2,i), '.b', 'linewidth', 10, 'markersize', 20);
end
end
axis equal tight
set(gca,'YTick',[-10 -5 0 5 10],'XTick',[-10 -5 0 5 10],persist.font.axis18{:});
plabel x '$x$'
plabel y '$y$'
set(get(gca,'ylabel'),'rotation',0)
% title 'Normalized electric field between two electrically charged nodes' interpreter latex
% title 'Elektromosan felt\"olt\"ott fegyverzetek (elektr\''od\''ak) \''altal keltett (normaliz\''alt) elektromos t\''er' interpreter latex
% legend([h1 h2], {'negative','positive'},'Position',[0.85,0.8,0.1,0.1])
persist.png('kondenzator')
text(0,6.3,['$Q_1 = -' num2str(Nr_anode/100) 'C$'],persist.font.latex18c{:})
text(0,-6.3,['$Q_2 = +' num2str(Nr_cathode/100) 'C$'],persist.font.latex18c{:})
title 'Elektr\''odok norm\''alt elektromos tere' interpreter latex
persist.png('kondenzator-szoveg')
Output:
│ - File saved to: /home/ppolcz/Repositories/Bitbucket/control-systems/zygote/dropbox_link/oktatas/anal3/1_vekanal/vectorfield_Coulombs_law/media/17_08_27_Time040457_runID3492_kondenzator.png │ - File saved to: /home/ppolcz/Repositories/Bitbucket/control-systems/zygote/dropbox_link/oktatas/anal3/1_vekanal/vectorfield_Coulombs_law/media/17_08_27_Time040457_runID3492_kondenzator-szoveg.png
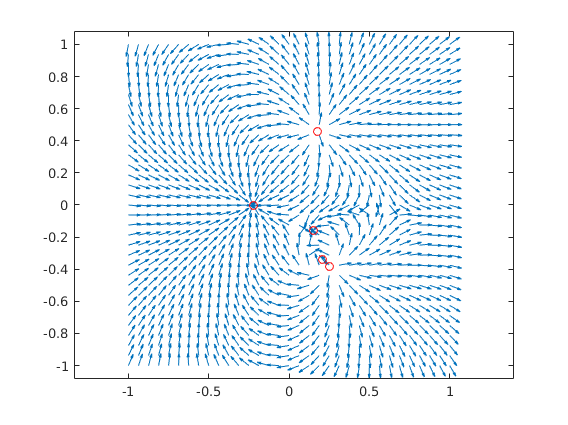
Komplex számos megközelítés - NAGYON SZÉP ('Bruno' megoldása)
n = 5; % number of charges
% locations
x = rand(n,1)-0.5;
y = rand(n,1)-0.5;
% charge
q = rand(n,1);
q = q - mean(q);
% Coulumb's number
ke = 8.9875517873681764e9;
xi = linspace(-1,1,33);
yi = linspace(-1,1,33);
[XI YI] = meshgrid(xi,yi);
zi = complex(XI,YI);
z = complex(x,y);
[ZI Z]=ndgrid(zi(:),z(:));
dZ = ZI-Z;
Zn = abs(dZ);
% http://en.wikipedia.org/wiki/Electric_field
E = (dZ./Zn.^3)*(q(:)*e*ke);
E = reshape(E, size(XI));
En = abs(E);
Ex = real(E);
Ey = imag(E);
figure
quiver(XI,YI,Ex./En,Ey./En);
hold on
plot(x, y, 'or')
axis equal
Próba: divergenciája az r/|r|^3 fuggvenynek
syms x y z t real
r = [x;y];
E = r / norm(r)^(3)
divE = trace(jacobian(E));
divE_fh = matlabFunction(divE, 'vars', {x,y});
[xx,yy] = meshgrid(linspace(-1,1,31));
divE_num = divE_fh(xx,yy)
surf(xx,yy,divE_num)
Output:
E = x/(abs(x)^2 + abs(y)^2)^(3/2) y/(abs(x)^2 + abs(y)^2)^(3/2) divE_num = 1.0e+03 * Columns 1 through 7 -0.0004 -0.0004 -0.0004 -0.0005 -0.0005 -0.0006 -0.0006 -0.0004 -0.0004 -0.0005 -0.0005 -0.0006 -0.0007 -0.0007 -0.0004 -0.0005 -0.0005 -0.0006 -0.0007 -0.0008 -0.0009 -0.0005 -0.0005 -0.0006 -0.0007 -0.0008 -0.0009 -0.0010 -0.0005 -0.0006 -0.0007 -0.0008 -0.0009 -0.0010 -0.0012 -0.0006 -0.0007 -0.0008 -0.0009 -0.0010 -0.0012 -0.0014 -0.0006 -0.0007 -0.0009 -0.0010 -0.0012 -0.0014 -0.0016 -0.0007 -0.0008 -0.0009 -0.0011 -0.0013 -0.0016 -0.0019 -0.0007 -0.0009 -0.0010 -0.0013 -0.0015 -0.0019 -0.0023 -0.0008 -0.0010 -0.0011 -0.0014 -0.0017 -0.0021 -0.0027 -0.0009 -0.0010 -0.0012 -0.0015 -0.0019 -0.0024 -0.0031 -0.0009 -0.0011 -0.0013 -0.0017 -0.0021 -0.0027 -0.0035 -0.0009 -0.0011 -0.0014 -0.0018 -0.0023 -0.0030 -0.0040 -0.0010 -0.0012 -0.0015 -0.0019 -0.0024 -0.0032 -0.0043 -0.0010 -0.0012 -0.0015 -0.0019 -0.0025 -0.0033 -0.0045 -0.0010 -0.0012 -0.0015 -0.0020 -0.0025 -0.0034 -0.0046 -0.0010 -0.0012 -0.0015 -0.0019 -0.0025 -0.0033 -0.0045 -0.0010 -0.0012 -0.0015 -0.0019 -0.0024 -0.0032 -0.0043 -0.0009 -0.0011 -0.0014 -0.0018 -0.0023 -0.0030 -0.0040 -0.0009 -0.0011 -0.0013 -0.0017 -0.0021 -0.0027 -0.0035 -0.0009 -0.0010 -0.0012 -0.0015 -0.0019 -0.0024 -0.0031 -0.0008 -0.0010 -0.0011 -0.0014 -0.0017 -0.0021 -0.0027 -0.0007 -0.0009 -0.0010 -0.0013 -0.0015 -0.0019 -0.0023 -0.0007 -0.0008 -0.0009 -0.0011 -0.0013 -0.0016 -0.0019 -0.0006 -0.0007 -0.0009 -0.0010 -0.0012 -0.0014 -0.0016 -0.0006 -0.0007 -0.0008 -0.0009 -0.0010 -0.0012 -0.0014 -0.0005 -0.0006 -0.0007 -0.0008 -0.0009 -0.0010 -0.0012 -0.0005 -0.0005 -0.0006 -0.0007 -0.0008 -0.0009 -0.0010 -0.0004 -0.0005 -0.0005 -0.0006 -0.0007 -0.0008 -0.0009 -0.0004 -0.0004 -0.0005 -0.0005 -0.0006 -0.0007 -0.0007 -0.0004 -0.0004 -0.0004 -0.0005 -0.0005 -0.0006 -0.0006 Columns 8 through 14 -0.0007 -0.0007 -0.0008 -0.0009 -0.0009 -0.0009 -0.0010 -0.0008 -0.0009 -0.0010 -0.0010 -0.0011 -0.0011 -0.0012 -0.0009 -0.0010 -0.0011 -0.0012 -0.0013 -0.0014 -0.0015 -0.0011 -0.0013 -0.0014 -0.0015 -0.0017 -0.0018 -0.0019 -0.0013 -0.0015 -0.0017 -0.0019 -0.0021 -0.0023 -0.0024 -0.0016 -0.0019 -0.0021 -0.0024 -0.0027 -0.0030 -0.0032 -0.0019 -0.0023 -0.0027 -0.0031 -0.0035 -0.0040 -0.0043 -0.0023 -0.0028 -0.0034 -0.0040 -0.0047 -0.0054 -0.0060 -0.0028 -0.0035 -0.0043 -0.0053 -0.0064 -0.0076 -0.0087 -0.0034 -0.0043 -0.0055 -0.0071 -0.0090 -0.0112 -0.0133 -0.0040 -0.0053 -0.0071 -0.0095 -0.0129 -0.0170 -0.0216 -0.0047 -0.0064 -0.0090 -0.0129 -0.0186 -0.0270 -0.0377 -0.0054 -0.0076 -0.0112 -0.0170 -0.0270 -0.0442 -0.0720 -0.0060 -0.0087 -0.0133 -0.0216 -0.0377 -0.0720 -0.1492 -0.0064 -0.0095 -0.0150 -0.0255 -0.0482 -0.1067 -0.3019 -0.0066 -0.0098 -0.0156 -0.0270 -0.0527 -0.1250 -0.4219 -0.0064 -0.0095 -0.0150 -0.0255 -0.0482 -0.1067 -0.3019 -0.0060 -0.0087 -0.0133 -0.0216 -0.0377 -0.0720 -0.1492 -0.0054 -0.0076 -0.0112 -0.0170 -0.0270 -0.0442 -0.0720 -0.0047 -0.0064 -0.0090 -0.0129 -0.0186 -0.0270 -0.0377 -0.0040 -0.0053 -0.0071 -0.0095 -0.0129 -0.0170 -0.0216 -0.0034 -0.0043 -0.0055 -0.0071 -0.0090 -0.0112 -0.0133 -0.0028 -0.0035 -0.0043 -0.0053 -0.0064 -0.0076 -0.0087 -0.0023 -0.0028 -0.0034 -0.0040 -0.0047 -0.0054 -0.0060 -0.0019 -0.0023 -0.0027 -0.0031 -0.0035 -0.0040 -0.0043 -0.0016 -0.0019 -0.0021 -0.0024 -0.0027 -0.0030 -0.0032 -0.0013 -0.0015 -0.0017 -0.0019 -0.0021 -0.0023 -0.0024 -0.0011 -0.0013 -0.0014 -0.0015 -0.0017 -0.0018 -0.0019 -0.0009 -0.0010 -0.0011 -0.0012 -0.0013 -0.0014 -0.0015 -0.0008 -0.0009 -0.0010 -0.0010 -0.0011 -0.0011 -0.0012 -0.0007 -0.0007 -0.0008 -0.0009 -0.0009 -0.0009 -0.0010 Columns 15 through 21 -0.0010 -0.0010 -0.0010 -0.0010 -0.0009 -0.0009 -0.0009 -0.0012 -0.0012 -0.0012 -0.0012 -0.0011 -0.0011 -0.0010 -0.0015 -0.0015 -0.0015 -0.0015 -0.0014 -0.0013 -0.0012 -0.0019 -0.0020 -0.0019 -0.0019 -0.0018 -0.0017 -0.0015 -0.0025 -0.0025 -0.0025 -0.0024 -0.0023 -0.0021 -0.0019 -0.0033 -0.0034 -0.0033 -0.0032 -0.0030 -0.0027 -0.0024 -0.0045 -0.0046 -0.0045 -0.0043 -0.0040 -0.0035 -0.0031 -0.0064 -0.0066 -0.0064 -0.0060 -0.0054 -0.0047 -0.0040 -0.0095 -0.0098 -0.0095 -0.0087 -0.0076 -0.0064 -0.0053 -0.0150 -0.0156 -0.0150 -0.0133 -0.0112 -0.0090 -0.0071 -0.0255 -0.0270 -0.0255 -0.0216 -0.0170 -0.0129 -0.0095 -0.0482 -0.0527 -0.0482 -0.0377 -0.0270 -0.0186 -0.0129 -0.1067 -0.1250 -0.1067 -0.0720 -0.0442 -0.0270 -0.0170 -0.3019 -0.4219 -0.3019 -0.1492 -0.0720 -0.0377 -0.0216 -1.1932 -3.3750 -1.1932 -0.3019 -0.1067 -0.0482 -0.0255 -3.3750 NaN -3.3750 -0.4219 -0.1250 -0.0527 -0.0270 -1.1932 -3.3750 -1.1932 -0.3019 -0.1067 -0.0482 -0.0255 -0.3019 -0.4219 -0.3019 -0.1492 -0.0720 -0.0377 -0.0216 -0.1067 -0.1250 -0.1067 -0.0720 -0.0442 -0.0270 -0.0170 -0.0482 -0.0527 -0.0482 -0.0377 -0.0270 -0.0186 -0.0129 -0.0255 -0.0270 -0.0255 -0.0216 -0.0170 -0.0129 -0.0095 -0.0150 -0.0156 -0.0150 -0.0133 -0.0112 -0.0090 -0.0071 -0.0095 -0.0098 -0.0095 -0.0087 -0.0076 -0.0064 -0.0053 -0.0064 -0.0066 -0.0064 -0.0060 -0.0054 -0.0047 -0.0040 -0.0045 -0.0046 -0.0045 -0.0043 -0.0040 -0.0035 -0.0031 -0.0033 -0.0034 -0.0033 -0.0032 -0.0030 -0.0027 -0.0024 -0.0025 -0.0025 -0.0025 -0.0024 -0.0023 -0.0021 -0.0019 -0.0019 -0.0020 -0.0019 -0.0019 -0.0018 -0.0017 -0.0015 -0.0015 -0.0015 -0.0015 -0.0015 -0.0014 -0.0013 -0.0012 -0.0012 -0.0012 -0.0012 -0.0012 -0.0011 -0.0011 -0.0010 -0.0010 -0.0010 -0.0010 -0.0010 -0.0009 -0.0009 -0.0009 Columns 22 through 28 -0.0008 -0.0007 -0.0007 -0.0006 -0.0006 -0.0005 -0.0005 -0.0010 -0.0009 -0.0008 -0.0007 -0.0007 -0.0006 -0.0005 -0.0011 -0.0010 -0.0009 -0.0009 -0.0008 -0.0007 -0.0006 -0.0014 -0.0013 -0.0011 -0.0010 -0.0009 -0.0008 -0.0007 -0.0017 -0.0015 -0.0013 -0.0012 -0.0010 -0.0009 -0.0008 -0.0021 -0.0019 -0.0016 -0.0014 -0.0012 -0.0010 -0.0009 -0.0027 -0.0023 -0.0019 -0.0016 -0.0014 -0.0012 -0.0010 -0.0034 -0.0028 -0.0023 -0.0019 -0.0016 -0.0013 -0.0011 -0.0043 -0.0035 -0.0028 -0.0023 -0.0019 -0.0015 -0.0013 -0.0055 -0.0043 -0.0034 -0.0027 -0.0021 -0.0017 -0.0014 -0.0071 -0.0053 -0.0040 -0.0031 -0.0024 -0.0019 -0.0015 -0.0090 -0.0064 -0.0047 -0.0035 -0.0027 -0.0021 -0.0017 -0.0112 -0.0076 -0.0054 -0.0040 -0.0030 -0.0023 -0.0018 -0.0133 -0.0087 -0.0060 -0.0043 -0.0032 -0.0024 -0.0019 -0.0150 -0.0095 -0.0064 -0.0045 -0.0033 -0.0025 -0.0019 -0.0156 -0.0098 -0.0066 -0.0046 -0.0034 -0.0025 -0.0020 -0.0150 -0.0095 -0.0064 -0.0045 -0.0033 -0.0025 -0.0019 -0.0133 -0.0087 -0.0060 -0.0043 -0.0032 -0.0024 -0.0019 -0.0112 -0.0076 -0.0054 -0.0040 -0.0030 -0.0023 -0.0018 -0.0090 -0.0064 -0.0047 -0.0035 -0.0027 -0.0021 -0.0017 -0.0071 -0.0053 -0.0040 -0.0031 -0.0024 -0.0019 -0.0015 -0.0055 -0.0043 -0.0034 -0.0027 -0.0021 -0.0017 -0.0014 -0.0043 -0.0035 -0.0028 -0.0023 -0.0019 -0.0015 -0.0013 -0.0034 -0.0028 -0.0023 -0.0019 -0.0016 -0.0013 -0.0011 -0.0027 -0.0023 -0.0019 -0.0016 -0.0014 -0.0012 -0.0010 -0.0021 -0.0019 -0.0016 -0.0014 -0.0012 -0.0010 -0.0009 -0.0017 -0.0015 -0.0013 -0.0012 -0.0010 -0.0009 -0.0008 -0.0014 -0.0013 -0.0011 -0.0010 -0.0009 -0.0008 -0.0007 -0.0011 -0.0010 -0.0009 -0.0009 -0.0008 -0.0007 -0.0006 -0.0010 -0.0009 -0.0008 -0.0007 -0.0007 -0.0006 -0.0005 -0.0008 -0.0007 -0.0007 -0.0006 -0.0006 -0.0005 -0.0005 Columns 29 through 31 -0.0004 -0.0004 -0.0004 -0.0005 -0.0004 -0.0004 -0.0005 -0.0005 -0.0004 -0.0006 -0.0005 -0.0005 -0.0007 -0.0006 -0.0005 -0.0008 -0.0007 -0.0006 -0.0009 -0.0007 -0.0006 -0.0009 -0.0008 -0.0007 -0.0010 -0.0009 -0.0007 -0.0011 -0.0010 -0.0008 -0.0012 -0.0010 -0.0009 -0.0013 -0.0011 -0.0009 -0.0014 -0.0011 -0.0009 -0.0015 -0.0012 -0.0010 -0.0015 -0.0012 -0.0010 -0.0015 -0.0012 -0.0010 -0.0015 -0.0012 -0.0010 -0.0015 -0.0012 -0.0010 -0.0014 -0.0011 -0.0009 -0.0013 -0.0011 -0.0009 -0.0012 -0.0010 -0.0009 -0.0011 -0.0010 -0.0008 -0.0010 -0.0009 -0.0007 -0.0009 -0.0008 -0.0007 -0.0009 -0.0007 -0.0006 -0.0008 -0.0007 -0.0006 -0.0007 -0.0006 -0.0005 -0.0006 -0.0005 -0.0005 -0.0005 -0.0005 -0.0004 -0.0005 -0.0004 -0.0004 -0.0004 -0.0004 -0.0004

end of the scope
Output:
└ 7.8604 [sec]