Tartalomjegyzék
\[ \newenvironment{dcases}{\left\{\begin{array}{ll}}{\end{array}\right.} \]Van der Pol egyszerűsített $\pi_a^{\left(e\right)} \left(x,\delta ,\delta^{˙} \right)$
Teljes Matlab script
(és live script)
kiegészítő függvényekkel.
Tekintsd meg LiveEditor nézetben is!
File: vdp_v7_egyszerusitett_Pia.m
Author: Peter Polcz (ppolcz@gmail.com)
Created on 2017. November 26.
% Automatically generated stuff
global SCOPE_DEPTH VERBOSE
SCOPE_DEPTH = 0;
VERBOSE = 0;
P_generate_symvars_v1_caller(2,0);
% define f(x):
e = 1;
A_sym = [
0 , -1
x1*x2 + 1 , -1
];
f_sym = expand(A_sym * x)
G_lfr = sym2lfr(A_sym);
lfr = P_lfrdata_v6(G_lfr);
lfr = P_LFR_reduction_v6(lfr, x);
Output:
f_sym =
-x2
x2*x1^2 + x1 - x2
A = lfr.A
B = lfr.B
Pi = lfr.Pi
Pib = lfr.Pib
n = numel(x);
p = numel(Pi);
m = numel(Pib);
Output:
A =
0 -1
1 -1
B =
0 0
1 0
Pi =
x1^2*x2
x1*x2
Pib =
x1
x2
x1^2*x2
x1*x2
dPi = expand(jacobian(Pi,x) * f_sym)
Pia = [Pib ; dPi]
Output:
dPi =
x1^4*x2 + x1^3 - x1^2*x2 - 2*x1*x2^2
x1^3*x2 + x1^2 - x1*x2 - x2^2
Pia =
x1
x2
x1^2*x2
x1*x2
x1^4*x2 + x1^3 - x1^2*x2 - 2*x1*x2^2
x1^3*x2 + x1^2 - x1*x2 - x2^2
Nb_sym = P_annihilator_linsolve_v6(Pib,x)
Na_sym = P_annihilator_linsolve_v6(Pia,x)
Na = matlabFunction(Na_sym,'vars',{x});
Nb = matlabFunction(Nb_sym,'vars',{x});
Output:
Nb_sym = [ x2, 0, 0, -1] [ 0, x1, 0, -1] [ 0, 0, 1, -x1] Na_sym = [ x1, -x2, x1, -1, 0, -1] [ x2, 0, 0, -1, 0, 0] [ 0, x1, 0, -1, 0, 0] [ 0, 0, 1, -x1, 0, 0] [ 0, 0, 0, x2, 1, -x1]
Aa = [
A B zeros(n,p)
zeros(p,m) eye(p)
];
P = sdpvar(m);
Pa = [ eye(m) ; zeros(p,m) ] * P * Aa;
R = (Pa' + Pa);
La = sdpvar(size(Na_sym,2),size(Na_sym,1),'full');
Lb = sdpvar(size(Nb_sym,2),size(Nb_sym,1),'full');
U = @(A) A + A';
X_v = [
-1.1463 -2.3221
-0.2645 -2.3221
1.7930 -0.2645
1.7930 0.9112
1.2051 2.3809
0.3233 2.3809
-1.7343 0.3233
-1.7343 -1.1463
-1.5227 -1.6840
-1.7950 -0.2723
-0.7462 -2.4000
-1.8555 -0.2218
0.8112 2.5000
-0.7296 -2.5204
-1.6480 -1.5306
-1.9133 -0.5306
1.9133 0.2449
1.5561 1.7245
1.6582 1.8469
-1.2194 0.8878
-1.3716 0.7544
1.3747 -0.7296
] * 0.8;
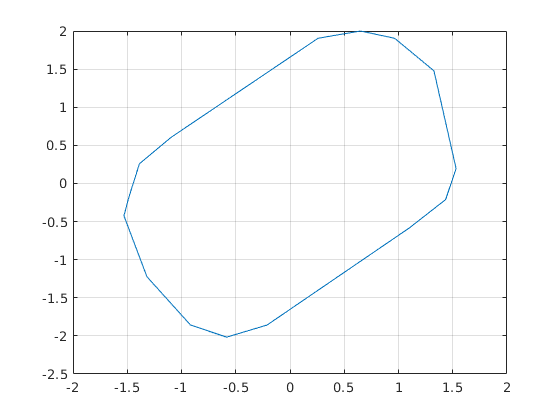
chull = convhull(X_v(:,1),X_v(:,2));
xv = X_v(chull,1);
yv = X_v(chull,2);
figure, plot(xv,yv), grid on
Constraints = [];
for i = 1:size(X_v,1)
w = X_v(i,:)';
Constraints = [ Constraints ...
P + U(Lb*Nb(w)) >= 0
R + U(La*Na(w)) <= 0
];
end
sol = optimize(Constraints)
Output:
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 52
Cones : 0
Scalar variables : 0
Matrix variables : 44
Integer variables : 0
Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator - tries : 0 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.00
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 52
Cones : 0
Scalar variables : 0
Matrix variables : 44
Integer variables : 0
Optimizer - threads : 4
Optimizer - solved problem : the primal
Optimizer - Constraints : 52
Optimizer - Cones : 0
Optimizer - Scalar variables : 0 conic : 0
Optimizer - Semi-definite variables: 44 scalarized : 682
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 1018 after factor : 1018
Factor - dense dim. : 0 flops : 2.91e+05
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 2.2e+01 1.0e+00 1.0e+00 0.00e+00 0.000000000e+00 0.000000000e+00 1.0e+00 0.02
1 5.5e+00 2.5e-01 5.0e-01 1.00e+00 0.000000000e+00 0.000000000e+00 2.5e-01 0.03
2 1.6e+00 7.2e-02 2.7e-01 1.00e+00 0.000000000e+00 0.000000000e+00 7.2e-02 0.03
3 6.3e-01 2.9e-02 1.7e-01 1.00e+00 0.000000000e+00 0.000000000e+00 2.9e-02 0.03
4 7.9e-02 3.6e-03 6.0e-02 1.00e+00 0.000000000e+00 0.000000000e+00 3.6e-03 0.04
5 4.3e-04 2.0e-05 4.4e-03 1.00e+00 0.000000000e+00 0.000000000e+00 2.0e-05 0.04
6 4.7e-11 2.1e-12 2.1e-12 1.00e+00 0.000000000e+00 0.000000000e+00 2.1e-12 0.04
Optimizer terminated. Time: 0.16
Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: 0.0000000000e+00 nrm: 5e-10 Viol. con: 1e-10 barvar: 9e-20
Dual. obj: 0.0000000000e+00 nrm: 2e+00 Viol. con: 0e+00 barvar: 2e-12
Optimizer summary
Optimizer - time: 0.16
Interior-point - iterations : 6 time: 0.04
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
sol =
struct with fields:
yalmiptime: 0.2529
solvertime: 0.1738
info: 'Successfully solved (MOSEK)'
problem: 0
sol
check(Constraints)
P = value(P);
R = value(R);
V_sym = Pib'*P*Pib;
% dV_sym = tPia'*R*tPia;
dV_sym = jacobian(V_sym,x)*f_sym;
V = matlabFunction(V_sym);
dV = matlabFunction(dV_sym);
xmin = min(X_v(:,1));
xmax = max(X_v(:,1));
ymin = min(X_v(:,2));
ymax = max(X_v(:,2));
res = 100;
xres = round((xmax - xmin) * res);
yres = round((ymax - ymin) * res);
[xx1,xx2] = meshgrid(linspace(xmin,xmax,xres), linspace(ymin,ymax,yres));
V_num = V(xx1,xx2);
dV_num = dV(xx1,xx2);
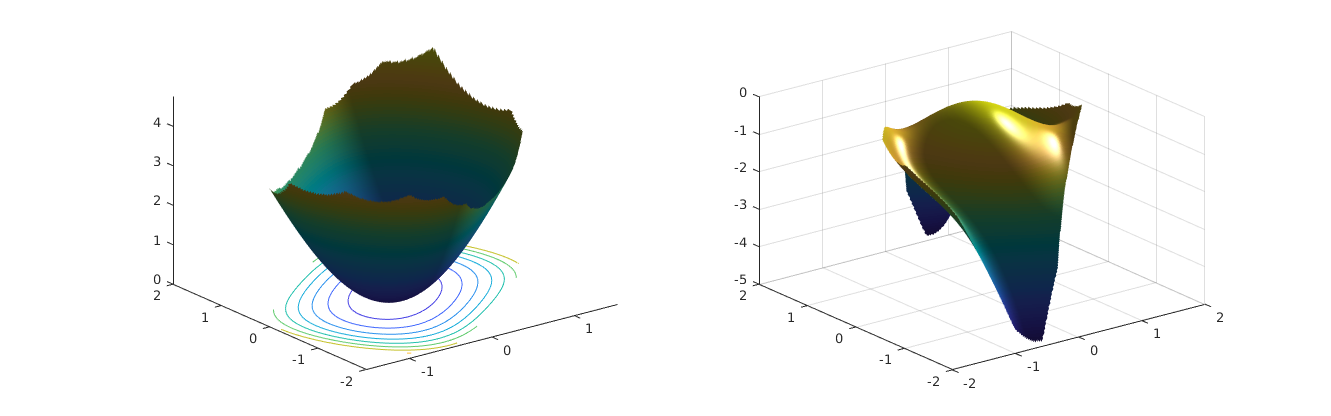
figure('Position', [ 276 433 1331 416 ], 'Color', [1 1 1]),
subplot(121), hold on
surf(xx1,xx2,V_num), shading interp; light
contour(xx1,xx2,V_num)
view([ -37.5 , 30 ])
subplot(122),
surf(xx1,xx2,dV_num), shading interp; light
Output:
sol =
struct with fields:
yalmiptime: 0.2529
solvertime: 0.1738
info: 'Successfully solved (MOSEK)'
problem: 0
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
| ID| Constraint| Primal residual| Dual residual|
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
| #1| Matrix inequality| 0.37842| 9.5991e-13|
| #2| Matrix inequality| 0.048157| 6.861e-13|
| #3| Matrix inequality| 0.45156| 8.3305e-13|
| #4| Matrix inequality| 0.039812| 5.371e-13|
| #5| Matrix inequality| 0.26263| 8.1209e-13|
| #6| Matrix inequality| 0.0075104| 7.7204e-13|
| #7| Matrix inequality| 0.27416| 7.4719e-13|
| #8| Matrix inequality| 0.036734| 5.0074e-13|
| #9| Matrix inequality| 0.36922| 7.5827e-13|
| #10| Matrix inequality| 0.039496| 7.0519e-13|
| #11| Matrix inequality| 0.49103| 8.2538e-13|
| #12| Matrix inequality| 0.025742| 3.4772e-13|
| #13| Matrix inequality| 0.32599| 7.7018e-13|
| #14| Matrix inequality| 0.008136| 6.8466e-13|
| #15| Matrix inequality| 0.32249| 8.2947e-13|
| #16| Matrix inequality| 0.042676| 6.4787e-13|
| #17| Matrix inequality| 0.35255| 9.0568e-13|
| #18| Matrix inequality| 0.051868| 7.4551e-13|
| #19| Matrix inequality| 0.3156| 7.717e-13|
| #20| Matrix inequality| 0.036537| 7.4291e-13|
| #21| Matrix inequality| 0.41808| 9.0507e-13|
| #22| Matrix inequality| 0.053264| 6.3829e-13|
| #23| Matrix inequality| 0.29657| 7.6783e-13|
| #24| Matrix inequality| 0.02242| 6.7639e-13|
| #25| Matrix inequality| 0.4283| 7.8694e-13|
| #26| Matrix inequality| 0.028204| -8.8674e-20|
| #27| Matrix inequality| 0.4083| 9.0221e-13|
| #28| Matrix inequality| 0.026841| 9.3425e-13|
| #29| Matrix inequality| 0.3308| 8.7891e-13|
| #30| Matrix inequality| 0.042479| 7.2418e-13|
| #31| Matrix inequality| 0.27983| 7.7432e-13|
| #32| Matrix inequality| 0.012526| 5.0385e-13|
| #33| Matrix inequality| 0.23843| 7.8881e-13|
| #34| Matrix inequality| 0.012151| 4.0557e-13|
| #35| Matrix inequality| 0.31962| 7.3682e-13|
| #36| Matrix inequality| 0.044969| 2.9032e-13|
| #37| Matrix inequality| 0.29272| 7.3548e-13|
| #38| Matrix inequality| 0.023739| 6.1944e-13|
| #39| Matrix inequality| 0.46878| 7.9055e-13|
| #40| Matrix inequality| 0.077407| 8.2064e-13|
| #41| Matrix inequality| 0.42751| 7.8493e-13|
| #42| Matrix inequality| 0.055244| 8.2772e-13|
| #43| Matrix inequality| 0.3679| 7.8819e-13|
| #44| Matrix inequality| 0.060539| 7.602e-13|
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
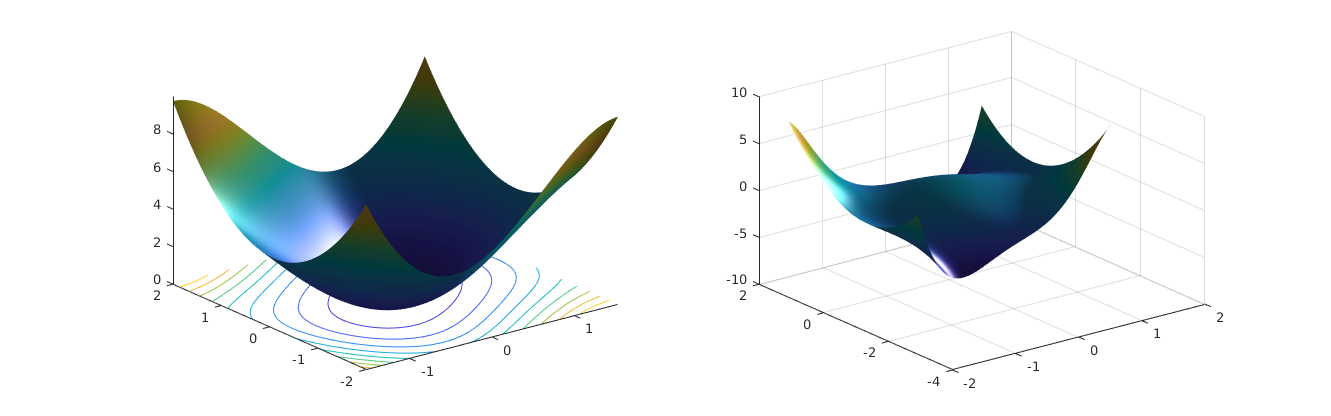
figure('Position', [ 276 433 1331 416 ], 'Color', [1 1 1]),
V_num(inpolygon(xx1,xx2,xv,yv) == 0) = NaN;
dV_num(inpolygon(xx1,xx2,xv,yv) == 0) = NaN;
subplot(121), hold on
surf(xx1,xx2,V_num), shading interp; light
contour(xx1,xx2,V_num)
view([ -37.5 , 30 ])
subplot(122),
surf(xx1,xx2,dV_num), shading interp; light