Tartalomjegyzék
\[ \newenvironment{dcases}{\left\{\begin{array}{ll}}{\end{array}\right.} \]Anal3 2017 2. félév - 3. gyakorlat. Segédszámítások
Teljes Matlab script
(és live script)
kiegészítő függvényekkel.
Tekintsd meg LiveEditor nézetben is!
Author: Péter Polcz ppolcz@gmail.com
Created on 2017. September 25.
2. feladat, felületintegrál
$s\left(u,v\right)=\left(\begin{array}{c}u\\v\\1-u-v\end{array}\right)$, ahol $u\in \left\lbrack 0,1\right\rbrack$ és $v\in \left\lbrack 0,1-u\right\rbrack$.
F = [ 1 ; 0 ; 0 ];
syms u v real
s = [ u ; v ; 1-u-v ];
dS = cross(diff(s,u),diff(s,v))
Integrand = double(dot(F,dS));
f_Integrand = @(u,v) Integrand + zeros(size(u));
integral2(f_Integrand,0,1,0,@(u) 1-u)
Output:
dS =
1
1
1
ans =
0.5000
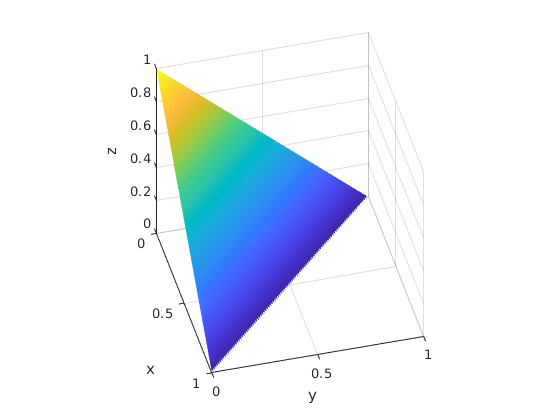
A felület, ami mentén integráltam:
s = matlabFunction(s(3));
[u,v] = meshgrid(0:0.01:1);
z = s(u,v);
z(u+v>1) = NaN;
surf(u,v,z), axis vis3d; shading interp
view([75.300 41.200])
xlabel('x')
ylabel('y')
zlabel('z')
4. feladat
syms u v real
syms x y z real
r = [x;y;z];
f = x + y + z;
s = [
u+v
u-v
u
];
fs = subs(f,r,s)
dS = norm(cross(diff(s,u),diff(s,v)))
I = fs*dS;
Output:
fs = 3*u dS = 6^(1/2)
Symbolical integration:
result = int(int(I,u,[0,1]),v,[0,1]), double(result)
Output:
result =
(3*6^(1/2))/2
ans =
3.6742
Numerical integration:
result = integral2(matlabFunction(I,'vars',{u v}),0,1,0,1)
Output:
result =
3.6742
6. feladat
syms u v R real
syms x y z real
r = [x;y;z];
F = [y;x;z];
s = [
R*cos(u)*sin(v)
R*sin(u)*sin(v)
R*cos(v)
];
dS = cross(diff(s,u),diff(s,v))
Fs = subs(F,r,s)
I = simplify(dot(Fs,dS))
result = int(int(I,u,0,2*pi),v,0,pi/2)
Output:
dS =
-R^2*cos(u)*sin(v)^2
-R^2*sin(u)*sin(v)^2
- R^2*cos(u)^2*cos(v)*sin(v) - R^2*cos(v)*sin(u)^2*sin(v)
Fs =
R*sin(u)*sin(v)
R*cos(u)*sin(v)
R*cos(v)
I =
-R^3*sin(v)*(2*cos(u)*sin(u) + cos(v)^2 - 2*cos(u)*cos(v)^2*sin(u))
result =
-(2*pi*R^3)/3
9. feladat (felületintegrál)
syms u v R real
syms x y z real
r = [x;y;z];
F = [x;y;z]/R;
F = [x;2*y;5*z];
s = [
R*cos(u)*sin(v)
R*sin(u)*sin(v)
R*cos(v)
];
dS = cross(diff(s,u),diff(s,v))
Fs = subs(F,r,s)
I = simplify(dot(Fs,dS))
result = int(int(I,u,0,2*pi),v,0,pi)
Output:
dS =
-R^2*cos(u)*sin(v)^2
-R^2*sin(u)*sin(v)^2
- R^2*cos(u)^2*cos(v)*sin(v) - R^2*cos(v)*sin(u)^2*sin(v)
Fs =
R*cos(u)*sin(v)
2*R*sin(u)*sin(v)
5*R*cos(v)
I =
-R^3*sin(v)*(sin(u)^2*sin(v)^2 - 4*sin(v)^2 + 5)
result =
-(32*pi*R^3)/3
9. feladat (térfogati integrál)
syms theta phi rho real
syms x y z real
r = [x;y;z];
R = 2;
F = [x;2*y;5*z];
divF = double(divergence(F,r));
Phi = [
rho*cos(theta)*sin(phi)
rho*sin(theta)*sin(phi)
rho*cos(phi)
];
Descartes koordinátákban kiszámolva:
$$\int_{-R}^R \int_{-\sqrt{R^2-x^2}}^{\sqrt{R^2-x^2}} \int_{-\sqrt{R^2-x^2-y^2}}^{\sqrt{R^2-x^2-y^2}} \nabla F(x,y,z) \,\mathrm{d} z \, \mathrm{d} y \, \mathrm{d}x$$
integral3(@(x,y,z) divF + zeros(size(x)),...
-R,R,...
@(x) -sqrt(R^2-x.^2),@(x) sqrt(R^2-x.^2),...
@(x,y) -sqrt(R^2-x.^2-y.^2),@(x,y) sqrt(R^2-x.^2-y.^2))
Output:
ans = 268.0826
Gömbi koordinátákban kiszámolva:
$$\int_0^R \int_0^\pi \int_0^{2\pi} \nabla F(\Phi(\rho,\vartheta,\varphi)) \cdot \Big|\det J(\rho,\vartheta,\varphi)\Big| \,\mathrm{d} \varphi\, \mathrm{d}\vartheta \, \mathrm{d}\rho$$
ahol $J(\rho,\vartheta,\varphi) = \mathrm{D}\,\Phi(\rho,\vartheta,\varphi)$ a $\Phi:\mathbb{R}^3 \to \mathbb{R}^3$ leképzés Jacobi mátrixa.
J = jacobian(Phi,[rho;theta;phi])
detJ = abs(simplify(det(J)))
Integrand = subs(divF,r,Phi)*detJ;
f_Integrand = matlabFunction(Integrand,'vars',[rho;theta;phi]);
integral3(f_Integrand,0,R,0,2*pi,0,pi)
Output:
J = [ cos(theta)*sin(phi), -rho*sin(phi)*sin(theta), rho*cos(phi)*cos(theta)] [ sin(phi)*sin(theta), rho*cos(theta)*sin(phi), rho*cos(phi)*sin(theta)] [ cos(phi), 0, -rho*sin(phi)] detJ = rho^2*abs(sin(phi)) ans = 268.0826
Ellenőrzésképpen
32*pi*R^3 / 3
Output:
ans = 268.0826