Tartalomjegyzék
\[ \newenvironment{dcases}{\left\{\begin{array}{ll}}{\end{array}\right.} \]Local Lyapunov function for a nontrivial equilibrium point
Teljes Matlab script kiegészítő függvényekkel.
Continuous-time Lotka-Volterra model
File: d2018_03_18_without_centering_lv2.m Directory: /1_projects/2_sta/demonstrative Author: Peter Polcz (ppolcz@gmail.com)
Created on 2018. March 18.
Model representation
A_sym = P_kiemel(f_sym-f0,x);
pcz_symeq(A_sym*x + f0, f_sym, 'Kiemeles jol tortent: A(x)*x + f0 = f(x)');
warning off
lfr = P_LFR_reduction_v6(P_lfrdata_v6(sym2lfr(A_sym)),x);
warning on
[A,B,Pi] = deal(lfr.A,lfr.B,lfr.Pi);
f0 = zeros(2,1);
Pib = [
1
x
Pi
];
Nb = P_annihilator_linsolve_v6(Pib,xd);
Pia = [
Pib
jacobian(Pi,x)*f_sym
];
Pia_A_sym = P_kiemel(Pia(2:end),x);
warning off
Pia_lfr = P_LFR_reduction_v6(sym2lfr(Pia_A_sym),x);
warning on
H = blkdiag(1, [ Pia_lfr.A Pia_lfr.B ]);
tPia = [ 1 ; Pia_lfr.Pib ];
% H = eye(numel(Pia));
% tPia = Pia;
pcz_symeq(H*tPia,Pia, 'H*tPia = Pia')
Na = P_annihilator_linsolve_v6(tPia,xdDd);
p = numel(Pi);
[q,m] = size(Nb);
[qa,ma] = size(Na);
Ea = [ eye(n+p+1) zeros(n+p+1,p) ];
Aa = [ zeros(1,1+n+2*p) ; blkdiag([f0 A B], eye(p)) ];
P = sdpvar(m);
L = sdpvar(m,q);
La = sdpvar(ma,qa);
R = H'*U(Ea'*P*Aa)*H;
xlim = [
0.2 1.8
0.2 1.8
];
X_v = allcomb(xlim(1,:),xlim(2,:));
Nb_fh = matlabFunction(Nb,'vars',{x});
Na_fh = matlabFunction(Na,'vars',{x});
Optimization
CONS = [];
isposdef = @(P) P >= 0;
% isposdef = @(P) P >= eye(size(P))*0.0001;
for i = 1:size(X_v,1)
x_num = X_v(i,:)';
CONS = [
CONS
isposdef( P + L*Nb_fh(x_num) + Nb_fh(x_num)'*L' )
isposdef( -R + La*Na_fh(x_num) + Na_fh(x_num)'*La' )
];
end
sol = optimize(CONS,[],sdpsettings('solver','mosek','verbose',false));
pcz_info(sol.problem == 0, sol.info);
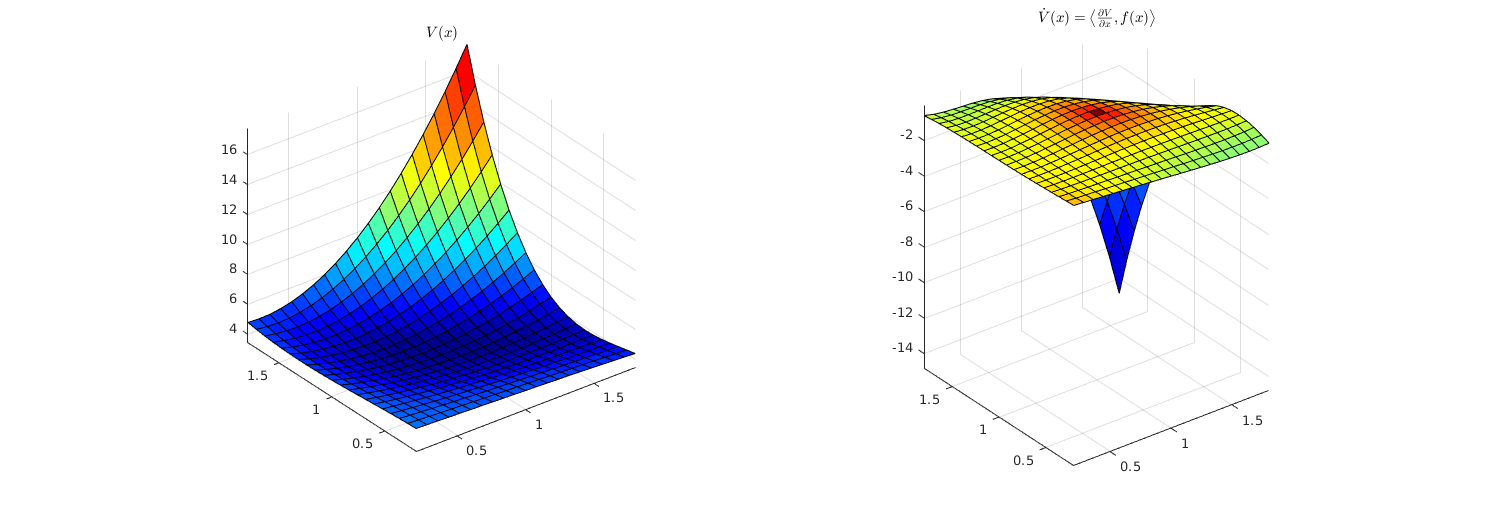
Visualization
Output:
┌d2018_03_18_without_centering_lv2 │ - Persistence for `d2018_03_18_without_centering_lv2` reused (inherited) [run ID: 0504, 2018.03.18. Sunday, 13:57:34] │ - Script `d2018_03_18_without_centering_lv2` backuped │ ┌P_generate_symvars_v1_caller │ └ 0.22016 [sec] │ [ OK ] Kiemeles jol tortent: A(x)*x + f0 = f(x) │ [ OK ] The first n elements of sigma_b must be identity permutation (in theory) │ [ OK ] The upper left (n+k)x(n+k) submatrix of Theta should be full-rank │ [ OK ] Equation of the permuted model should be the same │ [ OK ] Equation of the reduced model should be the same │ ┌P_annihilator_linsolve_v6 │ │ ┌P_annihilator_linsolve_v6 - core computation │ │ └ 0.080041 [sec] │ │ ┌P_annihilator_linsolve_v6 - quick check I. - obtained annihilator, prec: 10 │ │ │ - maximal difference: 6.245005e-17, row nr. 5 │ │ └ 0.048254 [sec] │ │ ┌P_annihilator_linsolve_v6 - beautify annihilator + !roundings! │ │ └ 0.00436 [sec] │ │ ┌P_annihilator_linsolve_v6 - quick check II. - the beautified annihilator, prec: 10 │ │ │ - maximal difference: 5.645239e-17, row nr. 2 │ │ └ 0.034158 [sec] │ └ 0.17135 [sec] │ [ OK ] The first n elements of sigma_b must be identity permutation (in theory) │ [ OK ] The upper left (n+k)x(n+k) submatrix of Theta should be full-rank │ [ OK ] Equation of the permuted model should be the same │ [ OK ] Equation of the reduced model should be the same │ [ OK ] H*tPia = Pia │ ┌P_annihilator_linsolve_v6 │ │ ┌P_annihilator_linsolve_v6 - core computation │ │ └ 0.14041 [sec] │ │ ┌P_annihilator_linsolve_v6 - quick check I. - obtained annihilator, prec: 10 │ │ │ - maximal difference: 4.770490e-17, row nr. 10 │ │ └ 0.056599 [sec] │ │ ┌P_annihilator_linsolve_v6 - beautify annihilator + !roundings! │ │ └ 0.010069 [sec] │ │ ┌P_annihilator_linsolve_v6 - quick check II. - the beautified annihilator, prec: 10 │ │ │ - maximal difference: 9.390229e-17, row nr. 2 │ │ └ 0.036706 [sec] │ └ 0.24836 [sec] │ [ OK ] Successfully solved (MOSEK) │ [ OK ] Positive semidefinite. Tolerance: 1e-05 │ [ OK ] Positive semidefinite. Tolerance: 1e-05 │ [ OK ] Positive semidefinite. Tolerance: 1e-05 │ [ OK ] Positive semidefinite. Tolerance: 1e-05 │ [ OK ] Positive semidefinite. Tolerance: 1e-05 │ [ OK ] Positive semidefinite. Tolerance: 1e-05 │ [ OK ] Positive semidefinite. Tolerance: 1e-05 │ [ OK ] Positive semidefinite. Tolerance: 1e-05 │ [ OK ] Egyenlo-e a ket kifejezes dV-re? └ 3.2957 [sec]