Tartalomjegyzék
\[ \newenvironment{dcases}{\left\{\begin{array}{ll}}{\end{array}\right.} \]Stabilitásvizsgálat diszkrét (proof of concepts)
Teljes Matlab script
(és live script)
kiegészítő függvényekkel.
Tekintsd meg LiveEditor nézetben is!
File: d2017_11_22_PoC.m
|Author: Peter Polcz (ppolcz@gmail.com) |
Created on 2017. November 22.
Automatically generated stuff
global SCOPE_DEPTH
SCOPE_DEPTH = 0;
ELSŐ PRÓBA [sikertelen]
Modell felállítása
P_generate_symvars_v5(2,1);
A = [
0 0.5
0.2 0.5
];
B = [
0 0.2
1 0
];
Pi = [
d1
x1^2
]
Pib = [x ; Pi];
f_sym = [A B] * Pib
N = P_annihilator_linsolve_v6(Pib,xd)
Output:
┌P_generate_symvars_v5
└ 0.42391 [sec]
Pi =
d1
x1^2
f_sym =
x1^2/5 + x2/2
d1 + x1/5 + x2/2
┌P_annihilator_linsolve_v6
│ - Persistence for `P_annihilator_linsolve_v6` initialized [run ID: 48, 113]Persistence for `2017.11.22. Wednesday, 11:36:32`
│ - Script `P_annihilator_linsolve_v6` backuped
│ ┌P_annihilator_linsolve_v6 - core computation
│ └ 0.075526 [sec]
│ ┌P_annihilator_linsolve_v6 - quick check I. - obtained annihilator, prec: 10
│ │ - maximal difference: 1.040834e-17, row nr. 3
│ └ 0.043203 [sec]
│ ┌P_annihilator_linsolve_v6 - beautify annihilator + !roundings!
│ └ 0.003057 [sec]
│ ┌P_annihilator_linsolve_v6 - quick check II. - the beautified annihilator, prec: 10
│ │ - maximal difference: 3.663112e-16, row nr. 2
│ └ 0.044435 [sec]
└ 0.19122 [sec]
N =
[ x1, 0, 0, -1]
[ x2, -x1, 0, 0]
[ d1, 0, -x1, 0]
[ 0, d1, -x2, 0]
Derivált
$$\pi_b[k+1] := \pi_b\big( x[k+1] \big) = \pi_b \Big( A x[k] + B \pi\big( x[k] \big) \Big) = \pi_b \big(f(x[k])\big)$$
Pi_next = expand(subs(Pi, x, f_sym))
Pia = [
Pib
Pi_next
]
Na = P_annihilator_linsolve_v6(Pia,xd)
Output:
Pi_next =
d1
x1^4/25 + (x1^2*x2)/5 + x2^2/4
Pia =
x1
x2
d1
x1^2
d1
x1^4/25 + (x1^2*x2)/5 + x2^2/4
┌P_annihilator_linsolve_v6
│ - Persistence for `P_annihilator_linsolve_v6` initialized [run ID: 48, 114]Persistence for `2017.11.22. Wednesday, 11:36:32`
│ - Script `P_annihilator_linsolve_v6` backuped
│ ┌P_annihilator_linsolve_v6 - core computation
│ └ 0.16248 [sec]
│ ┌P_annihilator_linsolve_v6 - quick check I. - obtained annihilator, prec: 10
│ │ - maximal difference: 1.908196e-16, row nr. 4
│ └ 0.080264 [sec]
│ ┌P_annihilator_linsolve_v6 - beautify annihilator + !roundings!
│ └ 0.007492 [sec]
│ ┌P_annihilator_linsolve_v6 - quick check II. - the beautified annihilator, prec: 10
│ │ - maximal difference: 1.422636e-17, row nr. 3
│ └ 0.10348 [sec]
└ 0.37813 [sec]
Na =
[ x1, 0, 0, -1, 0, 0]
[ x2, -x1, 0, 0, 0, 0]
[ d1, 0, 0, 0, -x1, 0]
[ 0, d1, 0, 0, -x2, 0]
[ 0, 0, 1, 0, -1, 0]
[ 0, 0, x1, 0, -x1, 0]
[ 0, 0, x2, 0, -x2, 0]
[ 0, 0, d1, 0, -d1, 0]
Optimalizáció
n = numel(x);
m = numel(Pib);
p = numel(Pi);
q = size(N,1);
P = sdpvar(m);
L = sdpvar(q,m);
La = sdpvar(numel(Pia),size(Na,1));
X_v = [
-1 -1
-1 1
1 1
1 -1
];
D_v = [
-1
1
] * 0.2;
Aa = [
A B zeros(n,p)
zeros(p,m) eye(p)
];
Ia = [eye(n) zeros(n,2*p) ; zeros(p,n) eye(p) zeros(p)];
Pa = Aa' * P * Aa - Ia' * P * Ia;
corners = unique(allcomb(X_v(:,1),X_v(:,2),D_v'),'rows');
Constraints = [];
for i = 1:size(corners,1)
N_num = double(subs(N,xd,corners(i,:)'));
Na_num = double(subs(Na,xd,corners(i,:)'));
Constraints = [Constraints , P + L*N_num + N_num'*L' >= 0.000*eye(size(P))];
Constraints = [Constraints , Pa + La*Na_num + Na_num'*La' <= 0];
end
sdpopts = sdpsettings('debug',1);
sol = optimize(Constraints, [], sdpopts);
Output:
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 68
Cones : 0
Scalar variables : 0
Matrix variables : 16
Integer variables : 0
Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator - tries : 0 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.00
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 68
Cones : 0
Scalar variables : 0
Matrix variables : 16
Integer variables : 0
Optimizer - threads : 4
Optimizer - solved problem : the primal
Optimizer - Constraints : 68
Optimizer - Cones : 0
Optimizer - Scalar variables : 0 conic : 0
Optimizer - Semi-definite variables: 16 scalarized : 248
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 1866 after factor : 1866
Factor - dense dim. : 0 flops : 2.18e+05
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 1.4e+01 1.0e+00 1.0e+00 0.00e+00 0.000000000e+00 0.000000000e+00 1.0e+00 0.00
1 2.3e+00 1.7e-01 4.1e-01 1.00e+00 0.000000000e+00 0.000000000e+00 1.7e-01 0.01
2 4.5e-01 3.3e-02 1.8e-01 1.00e+00 0.000000000e+00 0.000000000e+00 3.3e-02 0.01
3 1.1e-01 8.2e-03 8.8e-02 1.00e+00 0.000000000e+00 0.000000000e+00 8.2e-03 0.01
4 3.3e-02 2.4e-03 4.8e-02 1.00e+00 0.000000000e+00 0.000000000e+00 2.4e-03 0.02
5 5.5e-03 4.0e-04 1.9e-02 1.00e+00 0.000000000e+00 0.000000000e+00 4.0e-04 0.02
6 9.9e-04 7.2e-05 8.2e-03 1.00e+00 0.000000000e+00 0.000000000e+00 7.2e-05 0.02
7 1.6e-04 1.2e-05 3.3e-03 1.00e+00 0.000000000e+00 0.000000000e+00 1.2e-05 0.02
8 2.0e-05 1.5e-06 1.2e-03 1.00e+00 0.000000000e+00 0.000000000e+00 1.5e-06 0.02
9 1.1e-06 8.0e-08 2.7e-04 1.00e+00 0.000000000e+00 0.000000000e+00 7.8e-08 0.03
10 3.8e-09 2.9e-10 1.6e-05 1.00e+00 0.000000000e+00 0.000000000e+00 2.8e-10 0.03
Optimizer terminated. Time: 0.04
Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: 0.0000000000e+00 nrm: 1e+01 Viol. con: 2e-08 barvar: 0e+00
Dual. obj: 0.0000000000e+00 nrm: 1e+00 Viol. con: 0e+00 barvar: 3e-10
Optimizer summary
Optimizer - time: 0.04
Interior-point - iterations : 10 time: 0.03
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
sol
P = double(P)
Output:
sol =
struct with fields:
yalmiptime: 0.1118
solvertime: 0.0427
info: 'Successfully solved (MOSEK)'
problem: 0
P =
0.0000 -0.0000 0.0000 0.0000
-0.0000 0.0000 -0.0000 -0.0000
0.0000 -0.0000 1.1718 0.0000
0.0000 -0.0000 0.0000 -0.0000
MÁSODIK PRÓBA [siker: ha el nem hibáztam]
Modell felállítása
P_generate_symvars_v5(2,0);
A = [
0 0.5
0.2 0.5
];
B = [
0.2 0
0 0
];
Pi = [
x1*x2
x2^2
]
Pib = [x ; Pi];
f_sym = [A B] * Pib
N = P_annihilator_linsolve_v6(Pib,xd)
Output:
┌P_generate_symvars_v5
└ 0.26507 [sec]
Pi =
x1*x2
x2^2
f_sym =
x2/2 + (x1*x2)/5
x1/5 + x2/2
┌P_annihilator_linsolve_v6
│ - Persistence for `P_annihilator_linsolve_v6` initialized [run ID: 48, 115]Persistence for `2017.11.22. Wednesday, 11:36:34`
│ - Script `P_annihilator_linsolve_v6` backuped
│ ┌P_annihilator_linsolve_v6 - core computation
│ └ 0.080701 [sec]
│ ┌P_annihilator_linsolve_v6 - quick check I. - obtained annihilator, prec: 10
│ │ - maximal difference: 1.110223e-16, row nr. 2
│ └ 0.046574 [sec]
│ ┌P_annihilator_linsolve_v6 - beautify annihilator + !roundings!
│ └ 0.003109 [sec]
│ ┌P_annihilator_linsolve_v6 - quick check II. - the beautified annihilator, prec: 10
│ │ - maximal difference: 2.775558e-17, row nr. 3
│ └ 0.042349 [sec]
└ 0.19957 [sec]
N =
[ x2, 0, -1, 0]
[ 0, x1, -1, 0]
[ 0, x2, 0, -1]
[ 0, 0, x2, -x1]
Derivált
$$\pi_b[k+1] := \pi_b\big( x[k+1] \big) = \pi_b \Big( A x[k] + B \pi\big( x[k] \big) \Big) = \pi_b \big(f(x[k])\big)$$
Pi_next = expand(subs(Pi, x, f_sym))
Pia = [
Pib
Pi_next
]
Na = P_annihilator_linsolve_v6(Pia,xd)
Output:
Pi_next =
(x1^2*x2)/25 + (x1*x2^2)/10 + (x1*x2)/10 + x2^2/4
x1^2/25 + (x1*x2)/5 + x2^2/4
Pia =
x1
x2
x1*x2
x2^2
(x1^2*x2)/25 + (x1*x2^2)/10 + (x1*x2)/10 + x2^2/4
x1^2/25 + (x1*x2)/5 + x2^2/4
┌P_annihilator_linsolve_v6
│ - Persistence for `P_annihilator_linsolve_v6` initialized [run ID: 48, 116]Persistence for `2017.11.22. Wednesday, 11:36:34`
│ - Script `P_annihilator_linsolve_v6` backuped
│ ┌P_annihilator_linsolve_v6 - core computation
│ └ 0.10194 [sec]
│ ┌P_annihilator_linsolve_v6 - quick check I. - obtained annihilator, prec: 10
│ │ - maximal difference: 6.938894e-17, row nr. 3
│ └ 0.092443 [sec]
│ ┌P_annihilator_linsolve_v6 - beautify annihilator + !roundings!
│ └ 0.006179 [sec]
│ ┌P_annihilator_linsolve_v6 - quick check II. - the beautified annihilator, prec: 10
│ │ - maximal difference: 6.522560e-16, row nr. 6
│ └ 0.064657 [sec]
└ 0.29052 [sec]
Na =
[ x1, 0, 0, 5*x1 + (25*x2)/2 - 25/4, 50, - 50*x2 - 25]
[ x2, 0, 0, 5/2 - (5*x2)/2 - x1, -10, 10*x2]
[ 0, x1, 0, 5/2 - (5*x2)/2 - x1, -10, 10*x2]
[ 0, x2, 0, -1, 0, 0]
[ 0, 0, 1, 5/2 - (5*x2)/2 - x1, -10, 10*x2]
[ 0, 0, x1, 5*x1 + (25*x2)/4, 0, -25*x2]
[ 0, 0, x2, -x1, 0, 0]
Optimalizáció
n = numel(x);
m = numel(Pib);
p = numel(Pi);
q = size(N,1);
P = sdpvar(m);
L = sdpvar(q,m);
La = sdpvar(numel(Pia),size(Na,1));
X_v = [
-1 -1
-1 1
1 1
1 -1
];
Aa = [
A B zeros(n,p)
zeros(p,m) eye(p)
];
Ia = [eye(n) zeros(n,2*p) ; zeros(p,n) eye(p) zeros(p)];
Pa = Aa' * P * Aa - Ia' * P * Ia;
corners = X_v;
Constraints = [];
for i = 1:size(corners,1)
N_num = double(subs(N,xd,corners(i,:)'));
Na_num = double(subs(Na,xd,corners(i,:)'));
Constraints = [Constraints , P + L*N_num + N_num'*L' >= 0.0001*eye(size(P))];
Constraints = [Constraints , Pa + La*Na_num + Na_num'*La' + 0.001*eye(size(Pa)) <= 0];
end
sdpopts = sdpsettings('debug',1);
sol = optimize(Constraints, [], sdpopts);
Output:
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 62
Cones : 0
Scalar variables : 0
Matrix variables : 8
Integer variables : 0
Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator - tries : 0 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.00
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 62
Cones : 0
Scalar variables : 0
Matrix variables : 8
Integer variables : 0
Optimizer - threads : 4
Optimizer - solved problem : the primal
Optimizer - Constraints : 62
Optimizer - Cones : 0
Optimizer - Scalar variables : 0 conic : 0
Optimizer - Semi-definite variables: 8 scalarized : 124
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 1533 after factor : 1533
Factor - dense dim. : 0 flops : 1.36e+05
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 6.8e+00 1.0e+00 9.7e-01 0.00e+00 -2.560000000e-02 0.000000000e+00 1.0e+00 0.00
1 4.8e-01 7.1e-02 2.6e-01 9.96e-01 -2.110257714e-03 0.000000000e+00 7.1e-02 0.01
2 1.9e-04 2.7e-05 5.1e-03 1.00e+00 -7.261013172e-07 0.000000000e+00 2.7e-05 0.01
3 1.3e-09 1.9e-10 1.9e-10 1.00e+00 -6.910326724e-12 0.000000000e+00 1.9e-10 0.01
Optimizer terminated. Time: 0.02
Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: -6.9103267242e-12 nrm: 5e-10 Viol. con: 8e-08 barvar: 0e+00
Dual. obj: 0.0000000000e+00 nrm: 1e+00 Viol. con: 0e+00 barvar: 2e-10
Optimizer summary
Optimizer - time: 0.02
Interior-point - iterations : 3 time: 0.01
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
sol
P = double(P)
Pa = double(Pa)
Output:
sol =
struct with fields:
yalmiptime: 0.1104
solvertime: 0.0253
info: 'Successfully solved (MOSEK)'
problem: 0
P =
0.9954 0.0533 0.0053 0.0288
0.0533 1.3747 0.0427 0.0126
0.0053 0.0427 1.0561 0.0688
0.0288 0.0126 0.0688 1.1046
Pa =
-0.9404 0.0895 -0.0031 -0.0288 0.0085 0.0025
0.0895 -0.7555 0.0622 -0.0126 0.0240 0.0207
-0.0031 0.0622 -1.0163 -0.0688 0.0011 0.0058
-0.0288 -0.0126 -0.0688 -1.1046 0 0
0.0085 0.0240 0.0011 0 1.0561 0.0688
0.0025 0.0207 0.0058 0 0.0688 1.1046
V = Pib' * P * Pib; V_rounded(x) = expand(pcz_roundPoly(V))
dV = Pia' * Pa * Pia;
V_fh = matlabFunction(V)
dV_fh = matlabFunction(dV)
[xx1,xx2] = meshgrid(linspace(-1,1,40));
figure
surf(xx1,xx2,V_fh(xx1,xx2))
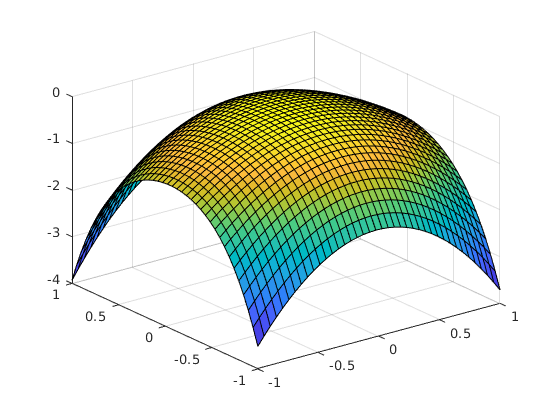
figure
surf(xx1,xx2,dV_fh(xx1,xx2))
Output:
V_rounded(x1, x2) =
(10561*x1^2*x2^2)/10000 + (10527*x1^2*x2)/1000000 + (6221*x1^2)/6250 + (2753*x1*x2^3)/20000 + (7151*x1*x2^2)/50000 + (2133*x1*x2)/20000 + (5523*x2^4)/5000 + (12629*x2^3)/500000 + (13747*x2^2)/10000
V_fh =
function_handle with value:
@(x1,x2)x1.*(x1.*9.953560184397977e-1+x2.*5.332463252148369e-2+x1.*x2.*5.263741392594083e-3+x2.^2.*2.884263149208525e-2)+x2.^2.*(x1.*2.884263149208525e-2+x2.*1.26291216131422e-2+x1.*x2.*6.882286268266789e-2+x2.^2.*1.104579799328212)+x2.*(x1.*5.332463252148369e-2+x2.*1.374702041023992+x1.*x2.*4.266977842201862e-2+x2.^2.*1.26291216131422e-2)+x1.*x2.*(x1.*5.263741392594083e-3+x2.*4.266977842201862e-2+x1.*x2.*1.0561325192881+x2.^2.*6.882286268266789e-2)
dV_fh =
function_handle with value:
@(x1,x2)(x1.*x2.*(1.0./5.0)+x1.^2.*(1.0./2.5e1)+x2.^2.*(1.0./4.0)).*(x1.*2.525824322628441e-3+x2.*2.073587655261373e-2+x1.*x2.*2.335667724323262e-1+x1.*x2.^2.*6.882286268266789e-3+x1.^2.*x2.*2.752914507306716e-3+x1.^2.*4.418319197312846e-2+x2.^2.*2.933506655027199e-1)+x1.*(x1.*(-9.40367936798838e-1)+x2.*8.947803483306389e-2-x1.*x2.*1.772195658768674e-3+x1.*x2.^2.*8.533955684403724e-4+x1.^2.*x2.*3.41358227376149e-4+x1.^2.*1.010329729051376e-4-x2.^2.*2.607768649032721e-2)+x2.*(x1.*8.947803483306389e-2-x2.*7.555252098973027e-1+x1.*x2.*6.87421379753629e-2+x1.*x2.^2.*2.396675990730635e-3+x1.^2.*x2.*9.586703962922541e-4+x1.^2.*8.29435062104549e-4-x2.^2.*1.453462498162182e-3)-x2.^2.*(x1.*2.884263149208525e-2+x2.*1.26291216131422e-2+x1.*x2.*6.882286268266789e-2+x2.^2.*1.104579799328212)+(x1.*x2.*(1.0./1.0e1)+x1.*x2.^2.*(1.0./1.0e1)+x1.^2.*x2.*(1.0./2.5e1)+x2.^2.*(1.0./4.0)).*(x1.*8.533955684403724e-3+x2.*2.396675990730635e-2+x1.*x2.*1.204305727438624e-1+x1.*x2.^2.*1.0561325192881e-1+x1.^2.*x2.*4.224530077152401e-2+x1.^2.*2.752914507306716e-3+x2.^2.*2.81238845492692e-1)+x1.*x2.*(x1.*(-3.130756091734735e-3)+x2.*6.219828667410952e-2-x1.*x2.*1.015059298462973+x1.*x2.^2.*1.052748278518817e-4+x1.^2.*x2.*4.210993114075266e-5+x1.^2.*2.30741051936682e-4-x2.^2.*6.711754403843393e-2)