Tartalomjegyzék

Script d2017_10_16_diszk_eloszlasok

Teljes Matlab script kiegészítő függvényekkel.

file:   d2017_10_16_diszk_eloszlasok.m
author: Peter Polcz <ppolcz@gmail.com>

Created on 2017. October 16.

Output:

┌d2017_10_16_diszk_eloszlasok
│   - Persistence for `d2017_10_16_diszk_eloszlasok` reused (inherited) [run ID: 8332, 2017.10.18. Wednesday, 08:50:32]
│   - Script `d2017_10_16_diszk_eloszlasok` backuped

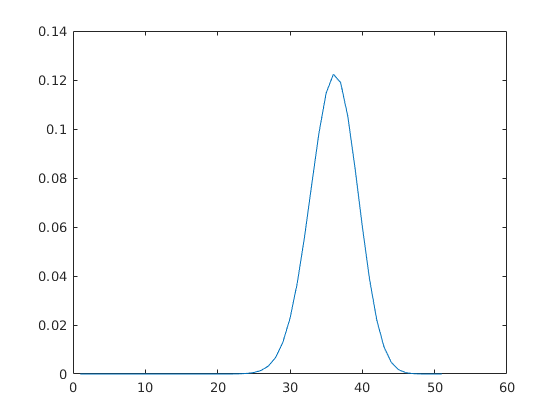
Binomialis eloszlas

n = 50;
p = 0.7;
k = num2cell(0:n);
nk = cellfun(@(k) nchoosek(n,k),k);
k = [k{:}];
plot(nk .* p.^k .* (1-p).^(n-k))

Poisson eloszlas

Derivation

Hipergeometrikus eloszlas vs Binomialis

Ezt irjak rola

The binomial distribution gives you the probability of x successes in n trials where the probability of success is p (that is, constant).

The hypergeometric distribution is exactly like the binomial distribution except that the probability changes with each trial.

Think of the binomial distribution as sampling with replacement and the hypergeometric distribution as sampling without replacement. Consider these examples.

Example 1: Sampling with replacement

Think of a box of marbles with 2 blue and 2 red. The probability of picking exactly 1 blue marble in 2 tries is equal to 1/2 (the probability of picking the blue marble) times 1/2 (the probability of picking the red marble) times 2 (the number of ways of picking 1 blue and 1 red marble) and this equals 1/2. Using the binomial distribution formula we have p(1) = 2C1 * (1/2)^1 * (1/2)^1 = 1/2.

Example 2: Sampling without replacement

Now think of the same box with the same marbles in it. This time when we pick a marble we don't put it back into the box. Then the probability of picking exactly 1 blue marble in 2 tries is given by 1/2 (picking the blue marble) * 2/3 (since there are 2 red and 1 blue left) PLUS 1/2 (picking the red marble first) * 2/3 (picking one of the two remaining blue marbles. This equals, 0.33 + 0.33 ~ 0.66. Using the hypergeometric distribution we have, p(1) = (2C1 * 2C1) / 4C2 ~ 0.66

Rossz kozelitessel binomialis

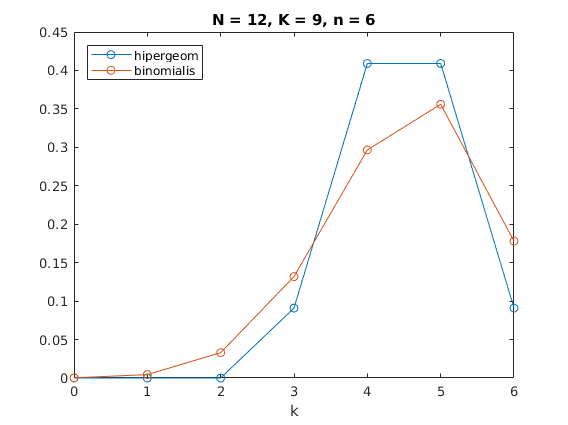
5. heti feladatsor, 3. pelda

N = 12; % osszesen
K = 9;  % gombolyu
n = 6;  % kivalasztunk

f = zeros(1,n+1);

for k = max(K-N+n,0):min(K,n)
    f(k+1) = nchoosek(K,k) / nchoosek(N,n) * nchoosek(N-K,n-k);
end
figure
plot(0:n,f,'o-'), hold on

p = K/N;
k = num2cell(0:n);
nk = cellfun(@(k) nchoosek(n,k),k);
k = [k{:}];
plot(0:n,nk .* p.^k .* (1-p).^(n-k),'o-')

L = legend('hipergeom','binomialis');
L.Location = 'northwest';

title(sprintf('N = %d, K = %d, n = %d',N,K,n))
xlabel k

Egyaltalan nem binomialis

5. heti feladatsor, 3. pelda modositva.

N = 12; % osszesen
K = 3;  % gombolyu
n = 10;  % kivalasztunk

f = zeros(1,n+1);

for k = max(K-N+n,0):min(K,n)
    f(k+1) = nchoosek(K,k) / nchoosek(N,n) * nchoosek(N-K,n-k);
end
figure
plot(0:n,f,'o-'), hold on

p = K/N;
k = num2cell(0:n);
nk = cellfun(@(k) nchoosek(n,k),k);
k = [k{:}];
plot(0:n,nk .* p.^k .* (1-p).^(n-k),'o-')

L = legend('hipergeom','binomialis');
L.Location = 'northeast';

title(sprintf('N = %d, K = %d, n = %d',N,K,n))
xlabel k

Jo kozelitessel binomialis

4. heti feladatsor, 6. pelda

N = 100; % osszesen
K = 80;  % van bankkartyaja
n = 10;  % kivalasztunk

f = zeros(1,n+1);

for k = max(K-N+n,0):min(K,n)
    f(k+1) = nchoosek(K,k) / nchoosek(N,n) * nchoosek(N-K,n-k);
end
figure
plot(0:n,f,'o-'), hold on

p = K/N;
k = num2cell(0:n);
nk = cellfun(@(k) nchoosek(n,k),k);
k = [k{:}];
plot(0:n,nk .* p.^k .* (1-p).^(n-k),'o-')

L = legend('hipergeom','binomialis');
L.Location = 'northwest';

title(sprintf('N = %d, K = %d, n = %d',N,K,n))
xlabel k

Megjobb kozelitessel binomialis

4. heti feladatsor, 6. pelda modositva

N = 1000; % osszesen
K = 600;  % van bankkartyaja
n = 40;  % kivalasztunk

f = zeros(1,n+1);

for k = max(K-N+n,0):min(K,n)
    f(k+1) = nchoosek(K,k) / nchoosek(N,n) * nchoosek(N-K,n-k);
end
figure
plot(0:n,f,'o-'), hold on

p = K/N;
k = num2cell(0:n);
nk = cellfun(@(k) nchoosek(n,k),k);
k = [k{:}];
plot(0:n,nk .* p.^k .* (1-p).^(n-k),'o-')

L = legend('hipergeom','binomialis');
L.Location = 'northwest';

title(sprintf('N = %d, K = %d, n = %d',N,K,n))
xlabel k

End of the script.

Output:

└ 3.3345 [sec]

Published with MATLAB® R2017b, and sanitarized by BeautifulSoup (Python script using BSoup is written by Polcz).