Tartalomjegyzék
\[ \newenvironment{dcases}{\left\{\begin{array}{ll}}{\end{array}\right.} \]Bioreaktor kimosódás
Teljes Matlab script
(és live script)
kiegészítő függvényekkel.
Tekintsd meg LiveEditor nézetben is!
Reviewed on 2017. September 26.
Azt vizsgálom, hogyan viselkedik a modell akkor, ha az $F_0$ bemenetnél nem ismerem a $\mu_{\mathrm{max}} =\delta$ értékét. Célom, hogy a rendszert $S_0$-ba stabilizáljam, ezért használok egy $F_0 =\frac{\delta_0 \text{ }S_0 \text{ }V}{q\left(S_0 \right)}$ bemenetet. Azonban $\delta_0$ csupán a nominális értéke a tényleges $\delta$-nak. Ilyen $F_0$ értékek mellett, minnél nagyobb $\delta_0$ és $\delta$ közti eltérés, annál jobb ki fog térni az egyensúlyi pont a ténylegestől. Ha ${\delta <\text{ }\delta }_0$ és nincs visszacsatolás, a biomassza kimosódik.
Következtetés
Ha csak egy kicsi intervallumon is mozog a $\delta \in \left\lbrack 0\ldotp 8,1\ldotp 2\right\rbrack$, akkor is olyan hatalmas mértékben mozog az egyensúlyi pont, hogy lehetetlenség ezt a Trofino módszerrel vizsgálni (az egyes deltákra kapott régiók nem fogják metszeni egymást). Az egyetlen megoldás, ha feltételezzük, hogy a működés során a $\delta$ értékét megbecsüljük (amúgyis, konstansnak feltételezzük).
global SCOPE_DEPTH
SCOPE_DEPTH = 0;
P_generate_symvars_v5(2,1);
syms X S V Sf Y K1 K2 d0 S0 k real
Output:
┌P_generate_symvars_v5 └ 0.39746 [sec]
Legyen $\mu \left(S\right)=\frac{\delta \text{ }S}{q\left(S\right)}$, ahol $q(S) = K_2 S^2 + S + K_1$, továbbá $\delta = \mu_{\text{max}}$.
q = @(S) K2*S.^2 + S + K1;
mu = @(S) d1 * S ./ q(S);
Equilibrium point ($S_0,X_0,F_0$)
X0 = (Sf - S0) * Y;
F0 = d0*S0*V / q(S0)
f(X,S,d1) = [
mu(S)*X - X*F0/V + k*(S-S0)*X/V
-mu(S)*X/Y + (Sf-S)*F0/V - k*(Sf-S)*(S-S0)/V
]
Ellenorzes_egyensulyi_pont = f(X0,S0,d0)
Output:
F0 =
(S0*V*d0)/(K2*S0^2 + S0 + K1)
f(X, S, d1) =
(S*X*d1)/(K2*S^2 + S + K1) - (S0*X*d0)/(K2*S0^2 + S0 + K1) + (X*k*(S - S0))/V
(k*(S - S0)*(S - Sf))/V - (S0*d0*(S - Sf))/(K2*S0^2 + S0 + K1) - (S*X*d1)/(Y*(K2*S^2 + S + K1))
Ellenorzes_egyensulyi_pont =
0
0
Optimális egyensúlyi pont:
S0_opt = 0.5 * (-2*K1 + 2*sqrt(K1^2 + Sf^2*K1*K2 + Sf*K1)) / (Sf*K2 + 1) == vpa(0.2187)
Output:
S0_opt = -(K1 - (K1^2 + K2*K1*Sf^2 + K1*Sf)^(1/2))/(K2*Sf + 1) == 0.2187
Numeric substitution
V = 4;
Sf = 10;
Y = 0.5;
K1 = 0.03;
K2 = 0.5;
d0 = 1;
% S0 = 0.5 * (-2*K1 + 2*sqrt(K1^2 + Sf^2*K1*K2 + Sf*K1)) / (Sf*K2 + 1);
S0 = 0.3;
X0 = double(subs(X0));
f_sym = subs(f(X,S,d1))
Ts = 0.1;
T = 10;
N = T / Ts;
f_fh = matlabFunction(f_sym,'vars',{t,[X ; S],d1,k});
Output:
f_sym =
(X*k*(S - 3/10))/4 - (4*X)/5 + (S*X*d1)/(S^2/2 + S + 3/100)
(k*(S - 10)*(S - 3/10))/4 - (4*S)/5 - (2*S*X*d1)/(S^2/2 + S + 3/100) + 8
Esettanulmány
Ha $k=0,\delta =1\ldotp 001$
k = 0;
d_real = 1.001;
f_ode = @(t,x) f_fh(t,x,d_real,k);
figure; hold on
[tt,xx] = ode45(f_ode, [0,T],[X0;S0]);
x0 = xx(end,:)';
xx = interp1(tt,xx,linspace(0,T,N));
plot(xx(:,1),xx(:,2),'.-');
plot(xx(1,1),xx(1,2),'o');
for i = 1:10
[~,xx] = ode45(f_ode, [0,T],x0+randn(2,1)*0.02);
plot(xx(:,1),xx(:,2),'-');
plot(xx(1,1),xx(1,2),'.');
end
text(X0+0.002,S0,'Egyensúliy pont [X0;S0] (lenne)')
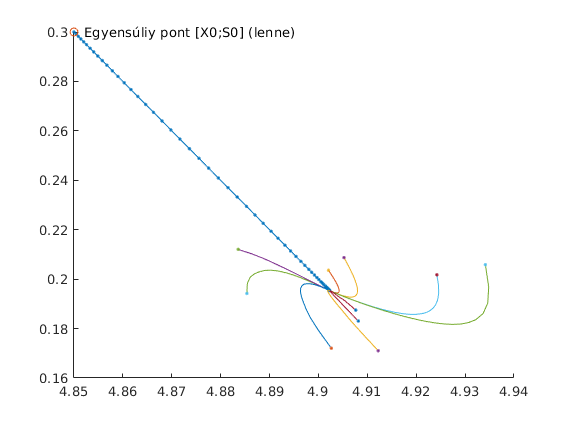
Ha $k=0,\delta =0\ldotp 999$, kimosódás
k = 0;
d_real = 0.999;
f_ode = @(t,x) f_fh(t,x,d_real,k);
figure; hold on
[tt,xx] = ode45(f_ode, [0,T],[X0;S0]);
x0 = xx(end,:)';
xx = interp1(tt,xx,linspace(0,T,N));
plot(xx(:,1),xx(:,2),'.-');
plot(xx(1,1),xx(1,2),'o');
for i = 1:10
[~,xx] = ode45(f_ode, [0,T],x0+randn(2,1)*0.02);
plot(xx(:,1),xx(:,2),'-');
plot(xx(1,1),xx(1,2),'.');
end
text(X0+0.002,S0,'Egyensúliy pont [X0;S0] (lenne)')

Ha $k=1,\delta =1\ldotp 01$
k = 1;
d_real = 1.01;
f_ode = @(t,x) f_fh(t,x,d_real,k);
figure; hold on
[tt,xx] = ode45(f_ode, [0,T],[X0;S0]);
x0 = xx(end,:)';
xx = interp1(tt,xx,linspace(0,T,N));
plot(xx(:,1),xx(:,2),'.-');
plot(xx(1,1),xx(1,2),'o');
for i = 1:10
[~,xx] = ode45(f_ode, [0,T],x0+randn(2,1)*0.02);
plot(xx(:,1),xx(:,2),'-');
plot(xx(1,1),xx(1,2),'.');
end
text(X0+0.002,S0,'Egyensúliy pont [X0;S0] (lenne)')
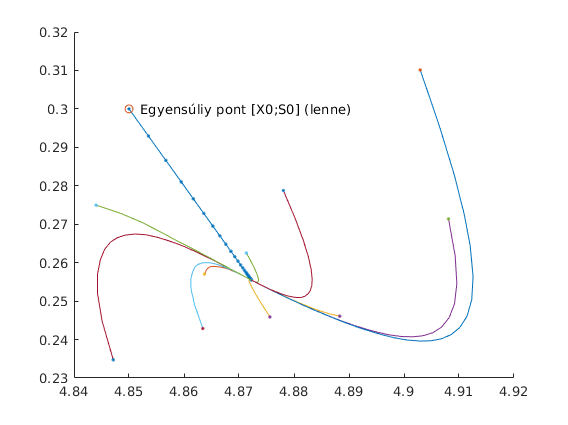
Ha $k=1,\delta =1\ldotp 1$
k = 1;
d_real = 1.1;
f_ode = @(t,x) f_fh(t,x,d_real,k);
figure; hold on
[tt,xx] = ode45(f_ode, [0,T],[X0;S0]);
x0 = xx(end,:)';
xx = interp1(tt,xx,linspace(0,T,N));
plot(xx(:,1),xx(:,2),'.-');
plot(xx(1,1),xx(1,2),'o');
for i = 1:10
[~,xx] = ode45(f_ode, [0,T],x0+randn(2,1)*0.02);
plot(xx(:,1),xx(:,2),'-');
plot(xx(1,1),xx(1,2),'.');
end
text(X0+0.002,S0,'Egyensúliy pont [X0;S0] (lenne)')

Ha $k=1,\delta =1\ldotp 2$, óriási kitérés
k = 1;
d_real = 1.2;
f_ode = @(t,x) f_fh(t,x,d_real,k);
figure; hold on
[tt,xx] = ode45(f_ode, [0,T],[X0;S0]);
x0 = xx(end,:)';
xx = interp1(tt,xx,linspace(0,T,N));
plot(xx(:,1),xx(:,2),'.-');
plot(xx(1,1),xx(1,2),'o');
for i = 1:10
[~,xx] = ode45(f_ode, [0,T],x0+randn(2,1)*0.02);
plot(xx(:,1),xx(:,2),'-');
plot(xx(1,1),xx(1,2),'.');
end
text(X0+0.002,S0,'Egyensúliy pont [X0;S0] (lenne)')

Ha $k=1,\delta =0\ldotp 99$, relatíve nagy kitérés
k = 1;
d_real = 0.99;
f_ode = @(t,x) f_fh(t,x,d_real,k);
figure; hold on
[tt,xx] = ode45(f_ode, [0,T],[X0;S0]);
x0 = xx(end,:)';
xx = interp1(tt,xx,linspace(0,T,N));
plot(xx(:,1),xx(:,2),'.-');
plot(xx(1,1),xx(1,2),'o');
for i = 1:10
[~,xx] = ode45(f_ode, [0,T],x0+randn(2,1)*0.02);
plot(xx(:,1),xx(:,2),'-');
plot(xx(1,1),xx(1,2),'.');
end
text(X0+0.002,S0,'Egyensúliy pont [X0;S0] (lenne)')
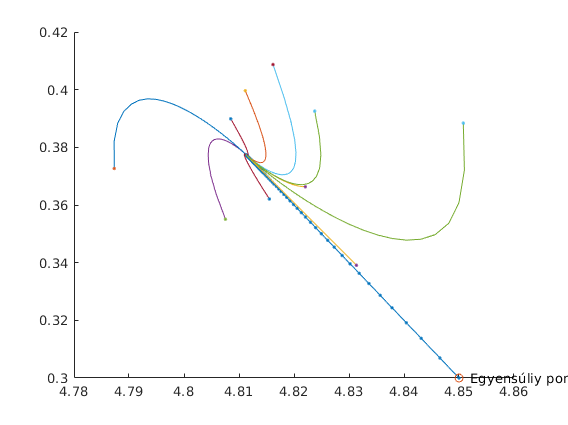
Ha $k=1,\delta =0\ldotp 9$, óriási kitérés $S$ szerint
k = 1;
d_real = 0.9;
f_ode = @(t,x) f_fh(t,x,d_real,k);
figure; hold on
[tt,xx] = ode45(f_ode, [0,T],[X0;S0]);
x0 = xx(end,:)';
xx = interp1(tt,xx,linspace(0,T,N));
plot(xx(:,1),xx(:,2),'.-');
plot(xx(1,1),xx(1,2),'o');
for i = 1:10
[~,xx] = ode45(f_ode, [0,T],x0+randn(2,1)*0.02);
plot(xx(:,1),xx(:,2),'-');
plot(xx(1,1),xx(1,2),'.');
end
text(X0+0.002,S0,'Egyensúliy pont [X0;S0] (lenne)')
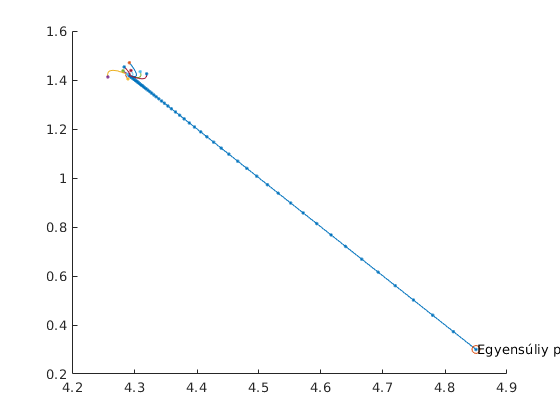
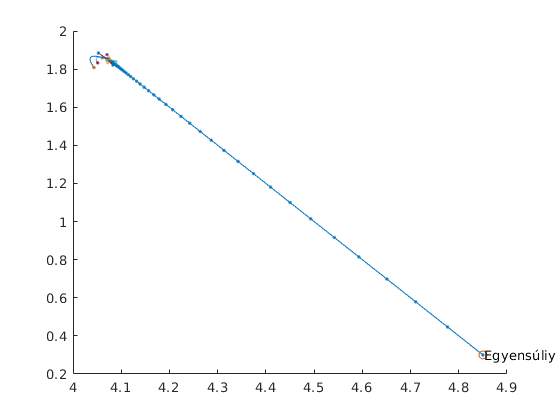
Ha $k=1,\delta =0\ldotp 8$, óriási kitérés $S$ szerint
k = 1;
d_real = 0.8;
f_ode = @(t,x) f_fh(t,x,d_real,k);
fig = figure; hold on
[tt,xx] = ode45(f_ode, [0,T],[X0;S0]);
x0 = xx(end,:)';
xx = interp1(tt,xx,linspace(0,T,N));
plot(xx(:,1),xx(:,2),'.-');
plot(xx(1,1),xx(1,2),'o');
for i = 1:10
[tt,xx] = ode45(f_ode, [0,T],x0+randn(2,1)*0.02);
plot(xx(:,1),xx(:,2),'-');
plot(xx(1,1),xx(1,2),'.');
end
text(X0+0.002,S0,'Egyensúliy pont [X0;S0] (lenne)')
Symbolic computations
syms X S X0 S0 d d0 k K2 K1 V Y Sf real
q = @(S) K2*S^2 + S + K1;
Expr = d*S*X/q(S) - d0*S0*X/q(S0) + k*(S-S0)*X/V
[num,den] = numden(Expr);
num = expand(num)
den
Output:
Expr = (S*X*d)/(K2*S^2 + S + K1) - (S0*X*d0)/(K2*S0^2 + S0 + K1) + (X*k*(S - S0))/V num = K1*S^2*X*k - K1*S0^2*X*k + K1^2*S*X*k - K1^2*S0*X*k - S*S0^2*X*k + S^2*S0*X*k + K1*S*V*X*d - K1*S0*V*X*d0 + S*S0*V*X*d - S*S0*V*X*d0 - K2^2*S^2*S0^3*X*k + K2^2*S^3*S0^2*X*k + K1*K2*S^3*X*k - K1*K2*S0^3*X*k - K2*S*S0^3*X*k + K2*S^3*S0*X*k + K1*K2*S*S0^2*X*k - K1*K2*S^2*S0*X*k + K2*S*S0^2*V*X*d - K2*S^2*S0*V*X*d0 den = V*(K2*S^2 + S + K1)*(K2*S0^2 + S0 + K1)