Tartalomjegyzék

Anal3 matlab konzi, 2017. november 7.

Teljes Matlab script (és live script) kiegészítő függvényekkel.
Tekintsd meg LiveEditor nézetben is!

syms x y z real

r = [x;y;z]
F = [
    y*z + 2
    x*z
    x*y
    ]
potential(F,r)

Output:

r =
 x
 y
 z
F =
 y*z + 2
     x*z
     x*y
ans =
x*(y*z + 2)

b = 1;
c = 1;
f = @(t,x) [
    x(2)
    -b * x(2) - c*x(1) + exp(-t)
    ];

x0 = [
    -1
    1
    ];

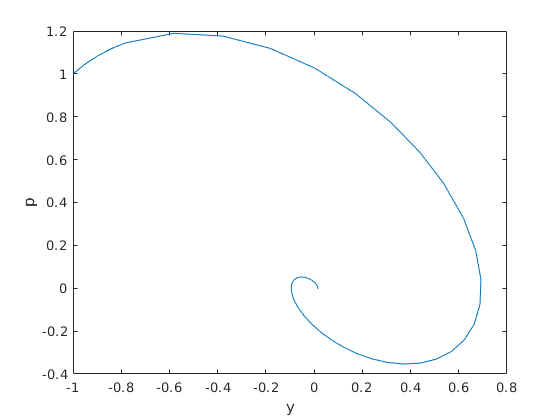
[t,x] = ode45(f, [0 10], x0);

plot(x(:,1),x(:,2))
xlabel y
ylabel p

syms t b c y p
x = [ y ; p ];

f = [
    p
    -b * p - c*y + exp(-t)
    ]
f = subs(f, [b c], [1 2])
f_fh = matlabFunction(f,'vars',{ t x })
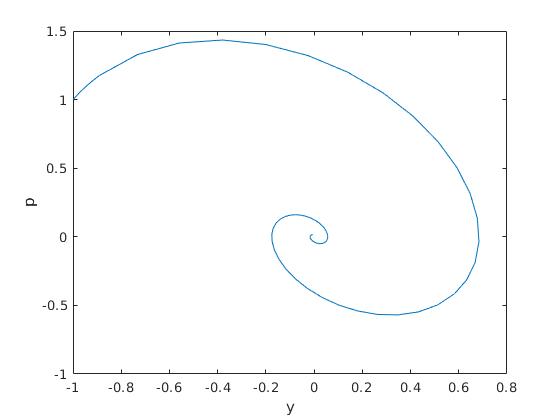
[t,x] = ode45(f_fh,[0,10],x0);
plot(x(:,1),x(:,2))
xlabel y
ylabel p

Output:

f =
                   p
 exp(-t) - b*p - c*y
f =
                 p
 exp(-t) - 2*y - p
f_fh =
  function_handle with value:
    @(t,in2)[in2(2,:);-in2(2,:)-in2(1,:).*2.0+exp(-t)]

Numerikus integralas

f = @(x) x.^2;

integral(f,0,2)
f = @(x,y) x.^2 + y.^2;
integral2(f,-1,1,@(x) -sqrt(1 - x.^2), @(x) sqrt(1 - x.^2))
f = @(x,y,z) x.^2 + y.^2 + sin(z);
integral3(f,-1,1,@(x) -sqrt(1 - x.^2), @(x) sqrt(1 - x.^2), ...
    @(x,y) -sqrt(1 - x.^2 - y.^2), @(x,y) sqrt(1 - x.^2 - y.^2))
f = @(y,x,z) x.^2 + y.^2 + sin(z);
integral3(f,-1,1,@(y) -sqrt(1 - y.^2), @(y) sqrt(1 - y.^2), ...
    @(y,x) -sqrt(1 - x.^2 - y.^2), @(y,x) sqrt(1 - x.^2 - y.^2))

Output:

ans =
    2.6667
ans =
    1.5708
ans =
    1.6755
ans =
    1.6755

Szimbolikus integralas

syms x y z C real

f = 1 / sqrt(x^2/C^2 - 1)
int(f,x), rewrite(acosh(x),'log')

Output:

f =
1/(x^2/C^2 - 1)^(1/2)
ans =
log(x + (x^2 - C^2)^(1/2))*(C^2)^(1/2)
ans =
log(x + (x - 1)^(1/2)*(x + 1)^(1/2))

Published with MATLAB® R2017b, and sanitarized by BeautifulSoup (Python script using BSoup is written by Polcz).