Tartalomjegyzék
\[ \newenvironment{dcases}{\left\{\begin{array}{ll}}{\end{array}\right.} \]DOA estimation for the Van der Pol model
Teljes Matlab script kiegészítő függvényekkel.
File: vanderpol_DOA.m Directory: 4_gyujtemegy/11_CCS/_1_ccs/ccs_2020/vanderpol Author: Peter Polcz (ppolcz@gmail.com)
Created on 2020. October 08. (2020b)
Van der Pol model
syms t x1 x2 real
x = [x1;x2];
f = [
-x2
-(1 - x1^2)*x2 + x1
];
M = [
0 -1 0 0
1 -1 0 1
];
E = [
1 0 0 0
0 1 0 0
];
phi = [
x1
x2
x1*x2
x1^2*x2
];
Check whether $f(x) = M \varphi(x)$.
ZEROS = simplify(f - M*phi)
Output:
ZEROS = 0 0
Annihilator for the Lagrange multiplier
N = [
x2 -x1 0 0
x2 0 -1 0
0 x1 -1 0
0 0 x1 -1
];
N_fh = matlabFunction(N,'vars',{ x });
Check whether $N(x) \varphi(x) = 0$
ZEROS = simplify(N*phi)
Output:
ZEROS = 0 0 0 0
Dimensions
n = numel(x);
m = numel(phi);
s = size(N,1);
The semidefinite program
Free symmetric Lyapunov matrix
P = sdpvar(n);
Lagrange multiplier as a full matrix variable
L = sdpvar(m,s,'full');
Corner points of polytope $\mathcal X$
X_v = [
-1 -1
-1 1
1 1
1 -1
]';
Constraints
CONS = [ P - eye(n) >= 0 ];
He = @(A) A.' + A;
for xi = X_v
CONS = [ CONS
He( E'*P*M + L*N_fh(xi) ) <= 0
];
end
Find a solution for the LMI constraints (withot any cost function to minimize)
sol = optimize(CONS)
Output:
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 19
Cones : 0
Scalar variables : 0
Matrix variables : 5
Integer variables : 0
Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator - tries : 0 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.00
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 19
Cones : 0
Scalar variables : 0
Matrix variables : 5
Integer variables : 0
Optimizer - threads : 4
Optimizer - solved problem : the primal
Optimizer - Constraints : 19
Optimizer - Cones : 0
Optimizer - Scalar variables : 0 conic : 0
Optimizer - Semi-definite variables: 5 scalarized : 43
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 190 after factor : 190
Factor - dense dim. : 0 flops : 1.08e+04
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 2.2e+00 2.0e+00 1.0e+00 0.00e+00 -2.000000000e+00 0.000000000e+00 1.0e+00 0.00
1 3.6e-01 3.2e-01 1.1e-01 -5.62e-01 -2.556982074e+00 0.000000000e+00 1.6e-01 0.01
2 5.8e-02 5.2e-02 2.9e-02 1.76e-01 -9.096761169e-01 0.000000000e+00 2.6e-02 0.02
3 1.1e-02 9.5e-03 1.3e-02 9.05e-01 -1.507737528e-01 0.000000000e+00 4.8e-03 0.02
4 1.9e-03 1.7e-03 5.4e-03 9.71e-01 -2.834863049e-02 0.000000000e+00 8.4e-04 0.02
5 4.2e-04 3.8e-04 2.6e-03 9.35e-01 -6.184615235e-03 0.000000000e+00 1.9e-04 0.02
6 9.1e-05 8.1e-05 1.5e-03 1.08e+00 -9.625375849e-04 0.000000000e+00 4.1e-05 0.02
7 2.3e-05 2.0e-05 6.2e-04 8.70e-01 -3.198515338e-04 0.000000000e+00 1.0e-05 0.02
8 6.3e-06 5.6e-06 3.5e-04 9.71e-01 -7.655566573e-05 0.000000000e+00 2.8e-06 0.02
9 1.4e-06 1.2e-06 1.6e-04 9.49e-01 -1.807785231e-05 0.000000000e+00 6.1e-07 0.02
10 3.5e-07 3.1e-07 8.3e-05 9.84e-01 -4.318160997e-06 0.000000000e+00 1.6e-07 0.02
11 8.2e-08 7.3e-08 4.0e-05 9.95e-01 -1.019376407e-06 0.000000000e+00 3.7e-08 0.02
12 2.8e-08 2.4e-08 2.4e-05 1.08e+00 -3.012976949e-07 0.000000000e+00 1.2e-08 0.02
13 7.1e-09 6.2e-09 1.2e-05 9.94e-01 -7.934255467e-08 0.000000000e+00 3.1e-09 0.02
14 2.0e-09 1.7e-08 6.4e-06 9.99e-01 -2.152107814e-08 0.000000000e+00 8.3e-10 0.03
Optimizer terminated. Time: 0.03
Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: -2.1521078138e-08 nrm: 2e+00 Viol. con: 4e-08 barvar: 0e+00
Dual. obj: 0.0000000000e+00 nrm: 5e+00 Viol. con: 0e+00 barvar: 7e-10
Optimizer summary
Optimizer - time: 0.03
Interior-point - iterations : 14 time: 0.03
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
sol =
struct with fields:
yalmipversion: '20200930'
matlabversion: '9.9.0.1467703 (R2020b)'
yalmiptime: 0.3961
solvertime: 0.0409
info: 'Successfully solved (MOSEK)'
problem: 0
Retain the solution
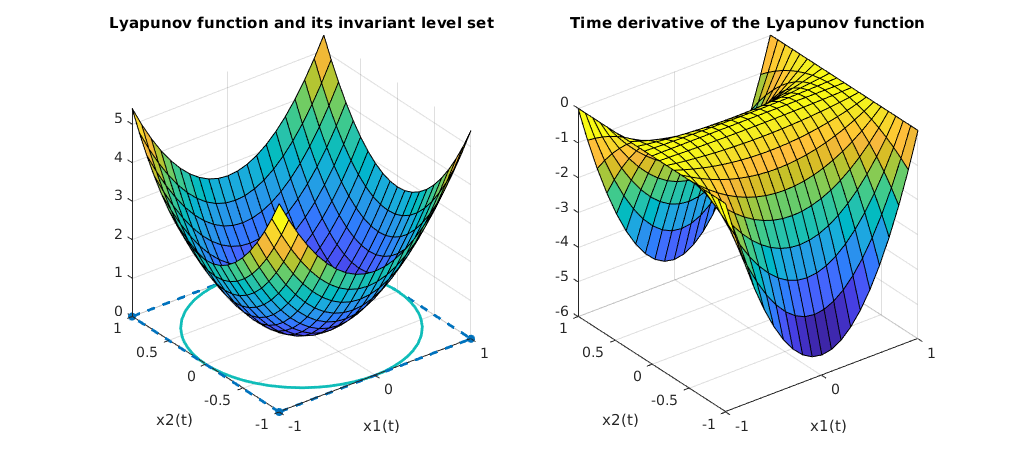
Here, we visualize the obtained Lyapunov function
P = value(P);
L = value(L);
V = x'*P*x;
dV = jacobian(V)*f;
V_fh = matlabFunction(V,'vars',x);
dV_fh = matlabFunction(dV,'vars',x);
[xx1,xx2] = meshgrid(-1:0.1:1);
VV = V_fh(xx1,xx2);
dVV = dV_fh(xx1,xx2);
alpha = find_alpha(VV);
fig = figure(1);
delete(fig.Children)
subplot(121);
surf(xx1,xx2,VV);
hold on
contour(xx1,xx2,VV,[1 1]*alpha,'LineWidth',2)
plot(X_v(1,[1:end 1]),X_v(2,[1:end 1]),'.--','MarkerSize',20,'LineWidth',2)
title('Lyapunov function and its invariant level set')
xlabel('x1(t)');
ylabel('x2(t)');
subplot(122);
surf(xx1,xx2,dVV)
title('Time derivative of the Lyapunov function')
xlabel('x1(t)');
ylabel('x2(t)');
Here, we illustrate how the LMI constraints look like. (The output of the cell is possibly moved to the end of this page.)
CONS
P_sym = gen_sym_symmetric('p',n);
L_sym = gen_sym_full('l',m,s);
for xi = X_v
display(N_fh(xi), sprintf('N(%g,%g)',xi))
display(He( E'*P_sym*M + L_sym*N_fh(xi) ), sprintf('LMI in (%g,%g) [this should be negative definite for some p_i and l_kj]',xi))
end
Output:
+++++++++++++++++++++++++++++++++++++++++++++++++++++ | ID| Constraint| Coefficient range| +++++++++++++++++++++++++++++++++++++++++++++++++++++ | #1| Matrix inequality 2x2| 1 to 1| | #2| Matrix inequality 4x4| 1 to 2| | #3| Matrix inequality 4x4| 1 to 2| | #4| Matrix inequality 4x4| 1 to 2| | #5| Matrix inequality 4x4| 1 to 2| +++++++++++++++++++++++++++++++++++++++++++++++++++++
Helper functions
These are some helper functions (not needed for optimization)
function [ret] = gen_sym_indexed(name, nr, startindex)
if nargin <= 2
startindex = 1;
end
indices = startindex:nr+startindex-1;
assert(numel(indices) == nr);
minwidth = min(floor(log10(indices)) + 1);
maxwidth = max(floor(log10(indices)) + 1);
ret = sym(zeros(1,nr));
for i = minwidth:maxwidth
tmp = sym([ name repmat('0',[1, maxwidth-i]) ],[10^i-1 , 1]);
ami_kell = max(startindex,10^(i-1)):min(nr+startindex,10^i)-1;
ret(ami_kell-startindex+1) = tmp(ami_kell);
end
end
function [ret] = gen_sym_full(name,dim1,dim2,startindex)
if nargin < 4
startindex = 1;
end
syms = gen_sym_indexed(name,dim1*dim2,startindex);
ret = reshape(syms, [dim1,dim2]);
end
function P = gen_sym_symmetric(name,n,startindex)
if nargin < 3
startindex = 1;
end
nr = n*(n+1)/2;
p = gen_sym_indexed(name, nr, startindex);
U = triu(ones(n));
P = sym(U);
P(U == 1) = p;
P = P + triu(P,1).';
end
function alpha = find_alpha(VV)
alpha = min([
VV(:,1)' VV(:,end)' VV(1,:) VV(end,:)
])*0.999;
end
Output:
N(-1,-1) =
-1 1 0 0
-1 0 -1 0
0 -1 -1 0
0 0 -1 -1
LMI in (-1,-1) [this should be negative definite for some p_i and l_kj] =
[ 2*p2 - 2*l05 - 2*l01, l01 - l02 - l06 - l09 - p1 - p2 + p3, - l03 - l05 - l07 - l09 - l13, p2 - l08 - l13 - l04]
[l01 - l02 - l06 - l09 - p1 - p2 + p3, 2*l02 - 2*l10 - 2*p2 - 2*p3, l03 - l06 - l10 - l11 - l14, l04 - l12 - l14 + p3]
[ - l03 - l05 - l07 - l09 - l13, l03 - l06 - l10 - l11 - l14, - 2*l07 - 2*l11 - 2*l15, - l08 - l12 - l15 - l16]
[ p2 - l08 - l13 - l04, l04 - l12 - l14 + p3, - l08 - l12 - l15 - l16, -2*l16]
N(-1,1) =
1 1 0 0
1 0 -1 0
0 -1 -1 0
0 0 -1 -1
LMI in (-1,1) [this should be negative definite for some p_i and l_kj] =
[ 2*l01 + 2*l05 + 2*p2, l01 + l02 + l06 - l09 - p1 - p2 + p3, l03 - l05 + l07 - l09 - l13, l04 + l08 - l13 + p2]
[l01 + l02 + l06 - l09 - p1 - p2 + p3, 2*l02 - 2*l10 - 2*p2 - 2*p3, l03 - l06 - l10 - l11 - l14, l04 - l12 - l14 + p3]
[ l03 - l05 + l07 - l09 - l13, l03 - l06 - l10 - l11 - l14, - 2*l07 - 2*l11 - 2*l15, - l08 - l12 - l15 - l16]
[ l04 + l08 - l13 + p2, l04 - l12 - l14 + p3, - l08 - l12 - l15 - l16, -2*l16]
N(1,1) =
1 -1 0 0
1 0 -1 0
0 1 -1 0
0 0 1 -1
LMI in (1,1) [this should be negative definite for some p_i and l_kj] =
[ 2*l01 + 2*l05 + 2*p2, l02 - l01 + l06 + l09 - p1 - p2 + p3, l03 - l05 + l07 - l09 + l13, l04 + l08 - l13 + p2]
[l02 - l01 + l06 + l09 - p1 - p2 + p3, 2*l10 - 2*l02 - 2*p2 - 2*p3, l11 - l06 - l10 - l03 + l14, l12 - l04 - l14 + p3]
[ l03 - l05 + l07 - l09 + l13, l11 - l06 - l10 - l03 + l14, 2*l15 - 2*l11 - 2*l07, l16 - l12 - l15 - l08]
[ l04 + l08 - l13 + p2, l12 - l04 - l14 + p3, l16 - l12 - l15 - l08, -2*l16]
N(1,-1) =
-1 -1 0 0
-1 0 -1 0
0 1 -1 0
0 0 1 -1
LMI in (1,-1) [this should be negative definite for some p_i and l_kj] =
[ 2*p2 - 2*l05 - 2*l01, l09 - l02 - l06 - l01 - p1 - p2 + p3, l13 - l05 - l07 - l09 - l03, p2 - l08 - l13 - l04]
[l09 - l02 - l06 - l01 - p1 - p2 + p3, 2*l10 - 2*l02 - 2*p2 - 2*p3, l11 - l06 - l10 - l03 + l14, l12 - l04 - l14 + p3]
[ l13 - l05 - l07 - l09 - l03, l11 - l06 - l10 - l03 + l14, 2*l15 - 2*l11 - 2*l07, l16 - l12 - l15 - l08]
[ p2 - l08 - l13 - l04, l12 - l04 - l14 + p3, l16 - l12 - l15 - l08, -2*l16]