Tartalomjegyzék
\[ \newenvironment{dcases}{\left\{\begin{array}{ll}}{\end{array}\right.} \]Geometrical meaning of Lie derivative
Teljes Matlab script kiegészítő függvényekkel.
File: lie_geometrical_meaning.m Directory: 4_gyujtemegy/11_CCS/_2_nonlin-pannon/2018 Author: Peter Polcz (ppolcz@gmail.com)
Created on 2018. July 29.
Requirements
vekanal_subsmesh.m, vekanal_quiver_sym.m and pcz_arrow.m
syms t x1 x2 real
x = [ x1 ; x2 ];
Lie = @(f,h) jacobian(h,x) * f;
f = [
x2 + 0.4*x2*x1
-x1-x2 + 0.3*x1^2
];
h = sin(x1+x2^2)^2 + x2^2;
Lfh = Lie(f,h);
Lfh_fh = matlabFunction(Lfh,'vars',{x'});
$$L_f h(x) = 2\,\cos\left({x_{2}}^2+x_{1}\right)\,\sin\left({x_{2}}^2+x_{1}\right) \,\left(x_{2}+\frac{2\,x_{1}\,x_{2}}{5}\right)-\left(2\,x_{2}+4\,x_{2} \,\cos\left({x_{2}}^2+x_{1}\right)\,\sin\left({x_{2}}^2+x_{1}\right)\right) \,\left(-\frac{3\,{x_{1}}^2}{10}+x_{1}+x_{2}\right)$$
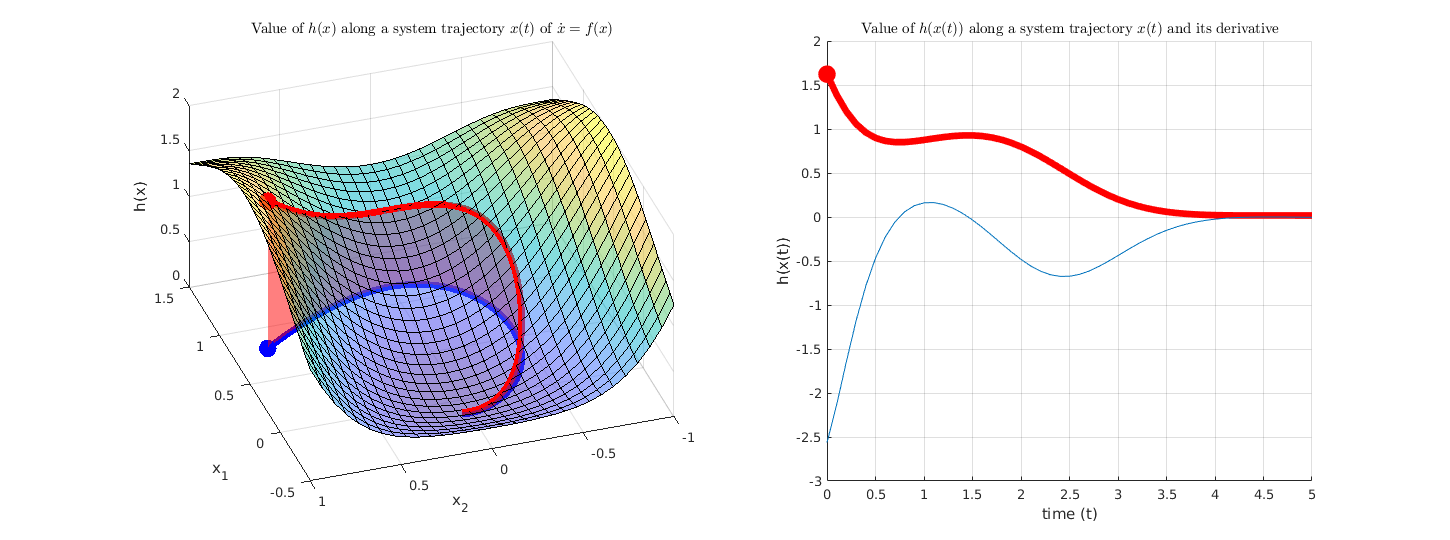
The blue line is a system trajectory of $\dot x = f(x)$ with the initial condition illustrated by the blue dot. The red line highlights the value of function $h(x)$ along the trajectory $x(t)$. In this way $h(x(t))$ can be considered as a scalar function of $t$. Its time derivative can be computed by the chain rule: $\frac{\mathrm{d}}{\mathrm{d} t} h(x(t)) = \frac{\partial h}{\partial x} \cdot \dot x = \frac{\partial h}{\partial x} f(x)$.
Geometrical meaning of the Lie bracket
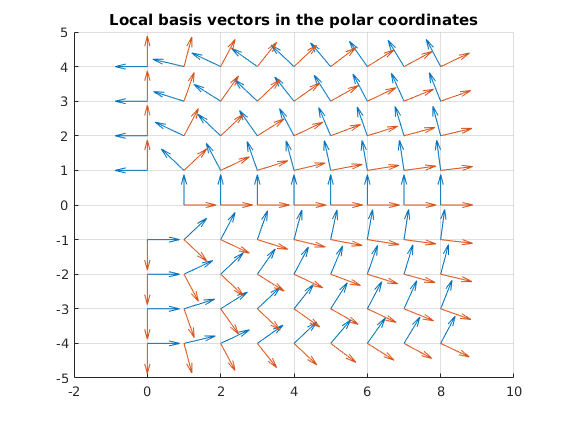
Local basis vectors in polar coordinates as two vector fields
syms x y real
Z = [x;y];
f_sym = [
-y
x
];
g_sym = [
x
y
] / sqrt(x^2 + y^2);
figure, hold on, grid on
Q1 = vekanal_quiver_sym(f_sym, Z, {0,8,9}, {-4,4,9}, 0.7);
Q2 = vekanal_quiver_sym(g_sym, Z, {0,8,9}, {-4,4,9}, 0.7);
title 'Local basis vectors in the polar coordinates'
Output:
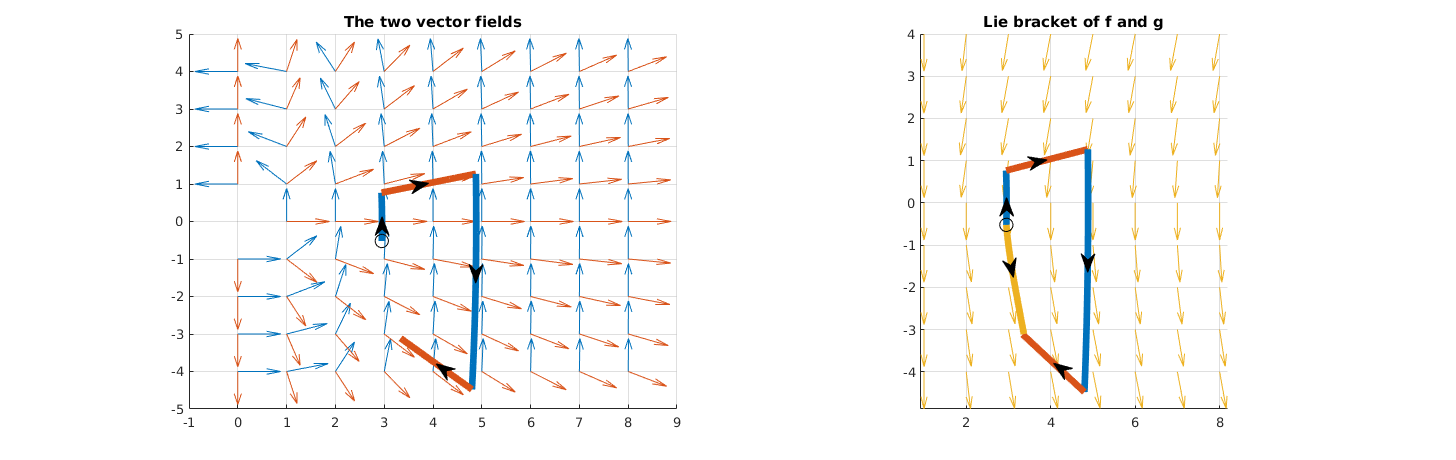
br_fg = 0 0 Path 1 starting from from (2.95,-0.52): - 0.4 seconds along the flow of f(x,y) - 1 seconds along the flow of g(x,y) - -0.4 seconds along the flow of f(x,y) (i.e. moving backwards) - -1 seconds along the flow of g(x,y) (i.e. moving backwards) Path 2 starting from from (1.88,-0.68): - 0.8 seconds along the flow of f(x,y) - 3 seconds along the flow of g(x,y) - -0.8 seconds along the flow of f(x,y) (i.e. moving backwards) - -3 seconds along the flow of g(x,y) (i.e. moving backwards) Path 3 starting from from (0.77,-0.64): - 1.4 seconds along the flow of f(x,y) - 5 seconds along the flow of g(x,y) - -1.4 seconds along the flow of f(x,y) (i.e. moving backwards) - -5 seconds along the flow of g(x,y) (i.e. moving backwards)
A walk along the flow of f and g and then backwards is closed.
What if the Lie bracket is non-zero
syms x y real
Z = [x;y];
f_sym = [
-y
x^3
];
g_sym = [
x
y
] / sqrt(x^2 + y^2);
br_fg = simplify(jacobian(g_sym,Z)*f_sym - jacobian(f_sym,Z)*g_sym);
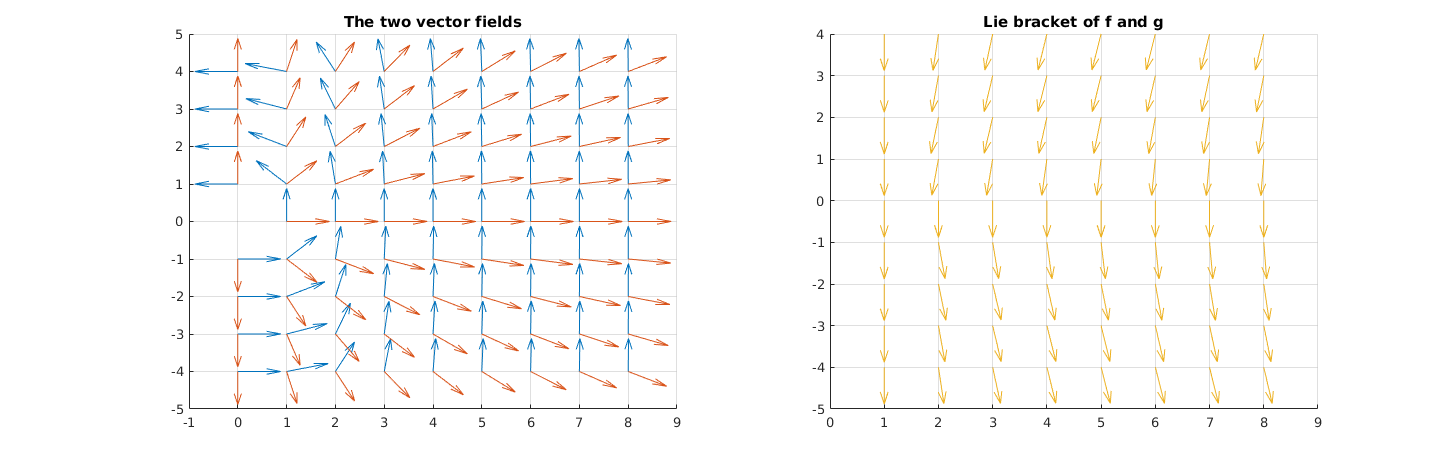
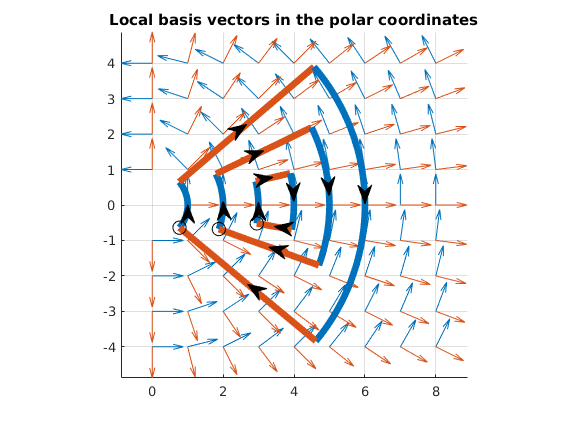
The walk along the flow of f and g is not closed
Output:
Path 1 starting from from (2.95,-0.52): - 0.05 seconds along the flow of f(x,y) - 2 seconds along the flow of g(x,y) - -0.05 seconds along the flow of f(x,y) (i.e. moving backwards) - -2 seconds along the flow of g(x,y) (i.e. moving backwards)