Tartalomjegyzék
\[ \newenvironment{dcases}{\left\{\begin{array}{ll}}{\end{array}\right.} \]Inverted pendulum, local linearization
Teljes Matlab script kiegészítő függvényekkel.
File: ccs_nonlin_ipend_localin.m Directory: 4_gyujtemegy/11_CCS/Modellek/inverse_pendulum/2018b_nonlin_pannon Author: Peter Polcz (ppolcz@gmail.com)
First created on 2017.05.02. Tuesday, 22:39:05 Modified on 2018. August 26.
Nonlinear model
% Time
syms t real
% State variables
syms position v phi omega real
% Input
syms u real
% State vector
x = [
position
v
phi
omega
];
% Known model parameters
M = 0.5;
m = 0.2;
l = 1;
g = 9.8;
b = 0;
q = 4*(M+m) - 3*m*cos(phi)^2;
f_sym = [
v
(4*m*l*sin(phi)*omega^2 - 1.5*m*g*sin(2*phi) -4*b*v) / q
omega
3*(-m*l*sin(2*phi)*omega^2 / 2 + (M+m)*g*sin(phi) + b*cos(phi)*v) / (l*q)
];
g_sym = [
0
4*l
0
-3*cos(phi)
] / (l*q);
Linearized model around the unstable equilibrium point
A = double(subs(jacobian(f_sym,x), x, [0;0;0;0]));
B = double(subs(g_sym, x, [0;0;0;0]));
C = [
1 0 0 0
0 0 1 0
];
D = [ 0 ; 0 ];
Static feedback design using LQR or pole placement
K = lqr(A,B,eye(4),1);
K = place(A,B,[-1+1i -1-1i -2+1i -2-1i]);
% Equation of the closed loop system
f_cls_sym = f_sym - g_sym*K*x;
% Simulation of the closed loop system
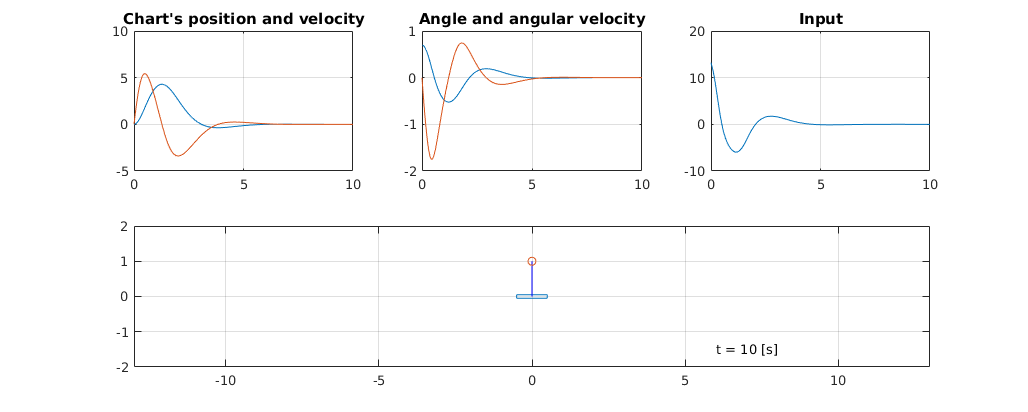
f_cls_ode = matlabFunction(f_cls_sym, 'vars', {t x});
[tt,xx] = ode45(f_cls_ode, [0 10], [0 0 0.7 0]');
uu = -K*xx';
% Visualization
ipend_simulate_0(tt,xx,uu)