Tartalomjegyzék

Script ccs2017_hf1_mo

Teljes Matlab script kiegészítő függvényekkel.

file:   ccs2017_hf1_mo.m
author: Peter Polcz <ppolcz@gmail.com>

Created on 2017. October 03.

Homework "in the red"

Define SSM matrices

A = [-2 -3 -8; 0 -3 -6; 0 1 -3];
B = [3; 1; -1];
C = [1 1 1];

Task 1. Computing D and S matrices

[S, D] = eig(A);

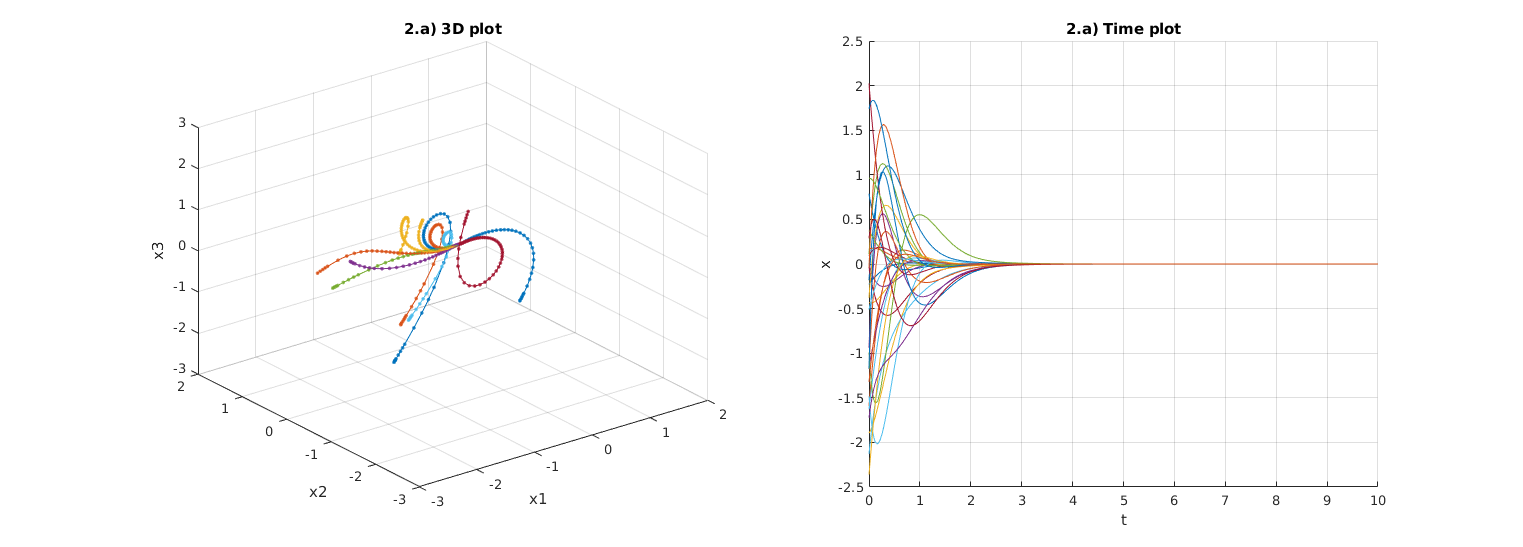
Task 2.a) Solving SSM

X0 = randn(10,3);
f1_dx = @(t,x) A*x + B*0;

figure('Position', [ 226 238 1523 547 ]);

subplot(121); hold on, grid on, view(3);
title '2.a) 3D plot'
xlabel('x1'); ylabel('x2'); zlabel('x3');

subplot(122); hold on, grid on;
title '2.a) Time plot'
xlabel('t'); ylabel('x');

for i = 1:10
    x0 = X0(i,:);
    [t,x] = ode45(f1_dx, [0 10], x0);

    subplot(121), plot3(x(:,1),x(:,2),x(:,3),'.-');
    subplot(122), plot(t,x(:,1),t,x(:,2),t,x(:,3));
end

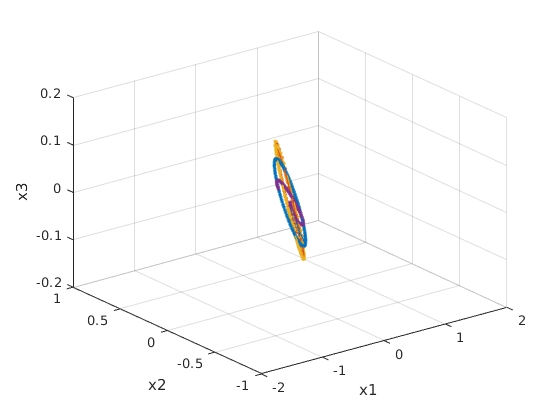
Task 2.b) Solving SSM

x0 = [0 0 0];
N = 4;
T = rand(N,1)*10;

fig3 = figure('Name','2.b) 3D plot','NumberTitle','off');
hold on, grid on;
xlabel('x1'); ylabel('x2'); zlabel('x3');
fig4 = figure('Name','2.b) Time plot','NumberTitle','off');
hold on, grid on;
xlabel('t'); ylabel('x');

for i = 1:N
    w0 = T(i);
    f2_dx = @(t,x) A*x + B*sin(w0*t);
    [t,x] = ode45(f2_dx, [0 10], x0);

    figure(fig3);
    plot3(x(:,1),x(:,2),x(:,3),'.-');
    view(3);

    figure(fig4);
    plot(t,x(:,1),t,x(:,2),t,x(:,3));
end

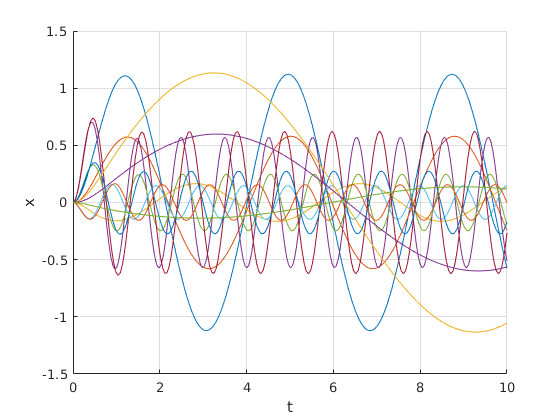
Task 3.

sys = ss(A,B,C,0);
figure('Name','h(t)','NumberTitle','off');
impulse(sys);

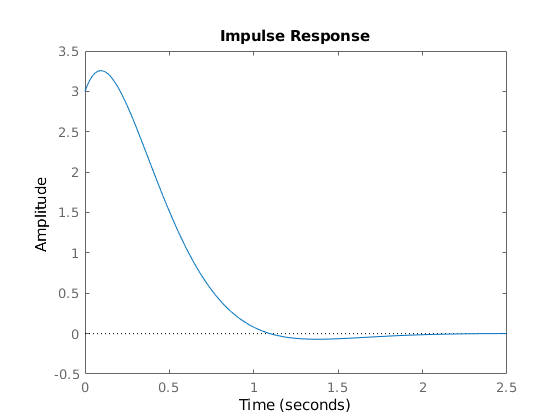
Task 4.

H = tf(sys)
[b,a] = ss2tf(A,B,C,0)

syms s
H_sym = poly2sym(b,s)/poly2sym(a,s)

Output:

H =
 
     3 s^2 + 30 s + 48
  -----------------------
  s^3 + 8 s^2 + 27 s + 30
 
Continuous-time transfer function.

b =
         0    3.0000   30.0000   48.0000
a =
     1     8    27    30
H_sym =
(3*s^2 + 30*s + 48)/(s^3 + 8*s^2 + 27*s + 30)

Auxiliary computations

Problem 1.

A = [
    -1 1 0
    0 -2 0
    2 1 -3
    ];

pcz_generateSymStateVector(3,'w');
pcz_latex(A*w)

[S,D] = eig(A)

A - S*D/S

Output:

\left(\begin{array}{c} w_{2}-w_{1} \\ -2w_{2} \\ 2w_{1}+w_{2}-3w_{3} \end{array}\right)
S =
         0    0.7071   -0.5774
         0         0    0.5774
    1.0000    0.7071   -0.5774
D =
    -3     0     0
     0    -1     0
     0     0    -2
ans =
   1.0e-15 *
         0         0         0
         0         0         0
         0    0.2220         0

S = [
    0 1 -1
    0 0 1
    1 1 -1
    ];

det(S)

iS = inv(S);

A
S*D*iS

pcz_num2str_latex(S)
pcz_num2str_latex(iS)

S*expm(sym(D))*iS - expm(sym(A))

pcz_latex(expm(sym(A)))

Output:

ans =
     1
A =
    -1     1     0
     0    -2     0
     2     1    -3
ans =
    -1     1     0
     0    -2     0
     2     1    -3
S = \pmqty{ 0 & 1 & -1 \\ 0 & 0 & 1 \\ 1 & 1 & -1 }
iS = \pmqty{ -1 & -0 & 1 \\ 1 & 1 & 0 \\ 0 & 1 & 0 }
ans =
[ 0, 0, 0]
[ 0, 0, 0]
[ 0, 0, 0]
\left(\begin{array}{ccc} e^{-1} & e^{-1}-e^{-2} & 0 \\ 0 & e^{-2} & 0 \\ e^{-1}-e^{-3} & e^{-1}-e^{-2} & e^{-3} \end{array}\right)

Published with MATLAB® R2017b, and sanitarized by BeautifulSoup (Python script using BSoup is written by Polcz).