Script anal3_diffgeom_tenzor_spherical_1
File: anal3_diffgeom_tenzor_spherical_1.m
Author: Peter Polcz ppolcz@gmail.com
Created on 2017.08.08. Tuesday, 14:34:51
Reviewed on 2017. November 08.
Contents
Index notation during the script
The name of a symbolic object 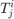 is chosen to be Ti_j
is chosen to be Ti_j
Ti_j = sym('T%d_%d',[2 2])
Ti_j = [ T1_1, T1_2] [ T2_1, T2_2]
The name of a symbolic object 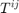 is chosen to be Tij
is chosen to be Tij
Tij = sym('T%d%d',[2 2])
Tij = [ T11, T12] [ T21, T22]
The name of a symbolic object 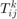 is chosen to be Tk_ij
is chosen to be Tk_ij
Tk_ij = sym('T%d_%d%d',[2 2 2])
Tk_ij(:,:,1) = [ T1_11, T1_21] [ T2_11, T2_21] Tk_ij(:,:,2) = [ T1_12, T1_22] [ T2_12, T2_22]
Variables of spherical coordinate system
Dimension of the vector space
n = 3;
Coordinates 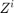 . During the script the name of variable representing coordinates
. During the script the name of variable representing coordinates 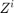 will be denoted by lower case letter 'z'. Coordinates:
will be denoted by lower case letter 'z'. Coordinates: 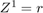 ,
, 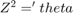 ,
, 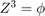 .
.
syms r theta phi real t = theta; p = phi; zi = [ r ; t ; p ]; % zi = sym('z%d',[n 1])
Mapping from Cartesian coordinate system to spherical.
R = [
r*cos(t)*sin(p)
r*sin(t)*sin(p)
r*cos(p)
]
R =
r*cos(theta)*sin(phi)
r*sin(phi)*sin(theta)
r*cos(phi)
Covariant basis vectors 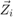 .
.
Zr = diff(R,r) Zt = diff(R,t) Zp = diff(R,p)
Zr =
cos(theta)*sin(phi)
sin(phi)*sin(theta)
cos(phi)
Zt =
-r*sin(phi)*sin(theta)
r*cos(theta)*sin(phi)
0
Zp =
r*cos(phi)*cos(theta)
r*cos(phi)*sin(theta)
-r*sin(phi)
Covariant basis vectors in a single operation.
Z_i = jacobian(R,zi)
Z_i = [ cos(theta)*sin(phi), -r*sin(phi)*sin(theta), r*cos(phi)*cos(theta)] [ sin(phi)*sin(theta), r*cos(theta)*sin(phi), r*cos(phi)*sin(theta)] [ cos(phi), 0, -r*sin(phi)]
Covariant metric tensor 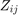 .
.
Z_ij = simplify(Z_i'*Z_i)
Z_ij = [ 1, 0, 0] [ 0, r^2*sin(phi)^2, 0] [ 0, 0, r^2]
Contravariant metric tensor 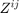 .
.
Zij = inv(Z_ij)
Zij = [ 1, 0, 0] [ 0, 1/(r^2*sin(phi)^2), 0] [ 0, 0, 1/r^2]
Contravariant components 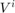 of vector field
of vector field 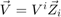 .
.
Vi = sym('V%d',[n 1]) syms V1(r,theta,phi) V2(r,theta,phi) V3(r,theta,phi) fVi = [ V1 ; V2 ; V3 ]; fVi = fVi(r,t,p) assume(in(fVi, 'real'))
Vi = V1 V2 V3 fVi = V1(r, theta, phi) V2(r, theta, phi) V3(r, theta, phi)
Convariant components  of vector field
of vector field 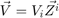 .
.
V_i = sym('V_%d',[n 1]) syms V_1(r,theta,phi) V_2(r,theta,phi) V_3(r,theta,phi) fV_i = [ V_1 ; V_2 ; V_3 ]; fV_i = fV_i(r,t,p) assume(in(fV_i, 'real') & in(fVi, 'real'))
V_i = V_1 V_2 V_3 fV_i = V_1(r, theta, phi) V_2(r, theta, phi) V_3(r, theta, phi)
Christoffel symbol 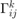
Denoted by 3-dimensional symbolic array Gamma(i,j,k).
Gamma = sym(zeros(n,n,n)); for i = 1:n for j = 1:n for k = 1:n for m = 1:n Gamma(i,j,k) = Gamma(i,j,k) + 0.5 * Zij(k,m) * ( ... diff(Z_ij(m,i), zi(j)) + diff(Z_ij(m,j), zi(i)) - diff(Z_ij(i,j), zi(m)) ... ); end end end end Gamma
Gamma(:,:,1) = [ 0, 0, 0] [ 0, -r*sin(phi)^2, 0] [ 0, 0, -r] Gamma(:,:,2) = [ 0, 1/r, 0] [ 1/r, 0, cos(phi)/sin(phi)] [ 0, cos(phi)/sin(phi), 0] Gamma(:,:,3) = [ 0, 0, 1/r] [ 0, -cos(phi)*sin(phi), 0] [ 1/r, 0, 0]
Covariant derivative 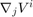
Using for loops
Covariant derivative of covariant tensor field  .
.
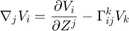
Using for loops (more transparent, clear-cut)
D_jfV_i = sym(zeros(n,n)); tic for i = 1:n for j = 1:n D_jfV_i(i,j) = diff(fV_i(i),zi(j)); for k = 1:n D_jfV_i(i,j) = D_jfV_i(i,j) + Gamma(i,j,k) * fV_i(k); end end end toc
Elapsed time is 0.375051 seconds.
Using matrix operations
With matrix operations the code is less transparent, but 10x faster.
Christoffel symbol demo for reshape operations
comb = allcomb(1:n,1:n,1:n);
comb = comb(:,[3 2 1]);
T = reshape(cellfun(@(a) {sprintf('(%d,%d,%d)', a)}, num2cell(comb,2)),[n,n,n])
3×3×3 cell array
T(:,:,1) =
{'(1,1,1)'} {'(1,2,1)'} {'(1,3,1)'}
{'(2,1,1)'} {'(2,2,1)'} {'(2,3,1)'}
{'(3,1,1)'} {'(3,2,1)'} {'(3,3,1)'}
T(:,:,2) =
{'(1,1,2)'} {'(1,2,2)'} {'(1,3,2)'}
{'(2,1,2)'} {'(2,2,2)'} {'(2,3,2)'}
{'(3,1,2)'} {'(3,2,2)'} {'(3,3,2)'}
T(:,:,3) =
{'(1,1,3)'} {'(1,2,3)'} {'(1,3,3)'}
{'(2,1,3)'} {'(2,2,3)'} {'(2,3,3)'}
{'(3,1,3)'} {'(3,2,3)'} {'(3,3,3)'}
Reshaped Christoffel symbol 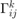 for multiplication along index
for multiplication along index 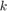 .
.
- First dimension:
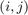
- Second simension:
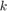
T2D_ij_k = reshape(T,[n^2 n])
T2D_ij_k =
9×3 cell array
{'(1,1,1)'} {'(1,1,2)'} {'(1,1,3)'}
{'(2,1,1)'} {'(2,1,2)'} {'(2,1,3)'}
{'(3,1,1)'} {'(3,1,2)'} {'(3,1,3)'}
{'(1,2,1)'} {'(1,2,2)'} {'(1,2,3)'}
{'(2,2,1)'} {'(2,2,2)'} {'(2,2,3)'}
{'(3,2,1)'} {'(3,2,2)'} {'(3,2,3)'}
{'(1,3,1)'} {'(1,3,2)'} {'(1,3,3)'}
{'(2,3,1)'} {'(2,3,2)'} {'(2,3,3)'}
{'(3,3,1)'} {'(3,3,2)'} {'(3,3,3)'}
Restore after multiplication along index 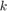 .
.
Restored_2tenzor = reshape(T2D_ij_k(:,1),[n n])
Restored_2tenzor =
3×3 cell array
{'(1,1,1)'} {'(1,2,1)'} {'(1,3,1)'}
{'(2,1,1)'} {'(2,2,1)'} {'(2,3,1)'}
{'(3,1,1)'} {'(3,2,1)'} {'(3,3,1)'}
Gamma2D_ij_k = reshape(Gamma,[n^2 n])
Gamma2D_ij_k = [ 0, 0, 0] [ 0, 1/r, 0] [ 0, 0, 1/r] [ 0, 1/r, 0] [ -r*sin(phi)^2, 0, -cos(phi)*sin(phi)] [ 0, cos(phi)/sin(phi), 0] [ 0, 0, 1/r] [ 0, cos(phi)/sin(phi), 0] [ -r, 0, 0]
Using reshape and matrix multiplication ()
tic
D_jfV_i_fast = reshape(Gamma2D_ij_k * fV_i, [n n]) + jacobian(fV_i,zi);
toc
pcz_info(pcz_symzero(D_jfV_i - D_jfV_i_fast), 'The two operations gave the same result')
Elapsed time is 0.008739 seconds. │ [ OK ] The two operations gave the same result
Permutation symbol
e_ijk = reshape(levicivita(comb,2), ones(1,n)*n)
e_ijk(:,:,1) =
0 0 0
0 0 1
0 -1 0
e_ijk(:,:,2) =
0 0 -1
0 0 0
1 0 0
e_ijk(:,:,3) =
0 1 0
-1 0 0
0 0 0